题目内容
【题目】已知:如图,AB为半圆O的直径,C是半圆O上一点,过点C作AB的平行线交⊙O于点E,连接AC、BC、AE,EB. 过点C作CG⊥AB于点G,交EB于点H.
(1)求证:∠BCG=∠EBG;
(2)若![]() ,求
,求![]() 的值.
的值.

【答案】(1)证明见解析;(2)3.
【解析】试题分析:(1)由圆周角定理的推论可知∠ACB=90°,由余角的性质可得∠CAB=∠BCG.根据CE∥AB可证∠CAB=∠ACE,再由等弧所对的圆周角相等可得∠ACE=∠EBG,从而可证明结论成立.
(2)由![]() 可得
可得![]() , 设GH=a,利用锐角三角函数的概念表示出GB=2a,CG=4a. 再根据△ECH∽△BGH可求出
, 设GH=a,利用锐角三角函数的概念表示出GB=2a,CG=4a. 再根据△ECH∽△BGH可求出![]() 的值.
的值.
证明:(1)∵AB是直径,
∴∠ACB=90°.
∵CG⊥AB于点G,
∴∠ACB=∠ CGB =90°.
∴∠CAB=∠BCG.
∵CE∥AB,
∴∠CAB=∠ACE.
∴∠BCG=∠ACE
又∵∠ACE=∠EBG
∴∠BCG=∠EBG.
(2)解:∵![]()
∴![]() ,
,
由(1)知,∠HBG =∠EBG =∠ACE =∠CAB
∴在Rt△HGB中, ![]() .
.
由(1)知,∠BCG =∠CAB
在Rt△BCG中, ![]() .
.
设GH=a,则GB=2a,CG=4a.CH=CG-HG=3a.
∵EC∥AB,
∴∠ECH =∠BGH,∠CEH =∠GBH
∴△ECH∽△BGH.
∴![]() .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
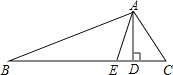
蓝天教育暑假优化学习系列答案【题目】如图,AB = 6cm,∠CAB = 25°,P是线段AB上一动点,过点P作PM⊥AB交射线AC于点M,连接MB,过点P作PN⊥MB于点N.设A,P两点间的距离为xcm,P,N两点间的距离为ycm.(当点P与点A或点B重合时,y的值均为0)小海根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.

下面是小海的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0.00 | 0.60 | 1.00 | 1.51 | 2.00 | 2.75 | 3.00 | 3.50 | 4.00 | 4.29 | 4.90 | 5.50 | 6.00 |
y/cm | 0.00 | 0.29 | 0.47 | 0.70 | 1.20 | 1.27 | 1.37 | 1.36 | 1.30 | 1.00 | 0.49 | 0.00 |
(说明:补全表格时相关数值保留两位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:当y=0.5时,与之对应的![]() 值的个数是 .
值的个数是 .