题目内容
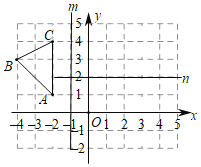
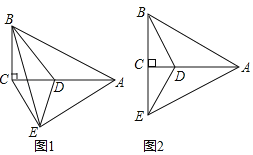
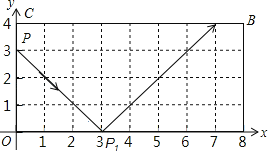
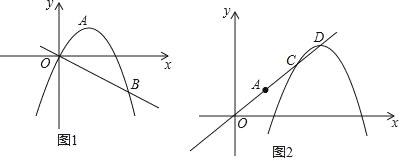
【题目】如图1,已知抛物线y=﹣x2+mx+m﹣2的顶点为A,且经过点B(3,﹣3).
(1)求顶点A的坐标
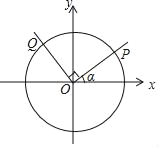
(2)若P是抛物线上且位于直线OB上方的一个动点,求△OPB的面积的最大值及比时点P的坐标;
(3)如图2,将原抛物线沿射线OA方向进行平移得到新的抛物线,新抛物线与射线OA交于C,D两点,请问:在抛物线平移的过程中,线段CD的长度是否为定值?若是,请求出这个定值;若不是,请说明理由.
【答案】(1)(﹣1,1);(2)P(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
(1)根据待定系数法,可得函数解析式,根据配方法,可得顶点坐标;
(2)过点P作y轴的平行线交OB与点Q,求出直线BP的解析式,表示出点Q的坐标,根据三角形的面积公式列出函数关系式,利用二次函数的最值可得P点坐标;
(3)根据平移规律,可得新抛物线,根据联立抛物线与OA的解析式,可得C、D点的横坐标,根据勾股定理,可得答案.
解:(1)把B(3,﹣3)代入y=﹣x2+mx+m2得:﹣3=﹣32+3m+m2,
解得m=2,
∴y=﹣x2+2x=﹣(x+1)2+1,
∴顶点A的坐标是(﹣1,1);
(2)过点P作y轴的平行线交OB与点Q.
∵直线OB的解析式为y=﹣x,
故设P(n,﹣n2+2n),Q(n,﹣n),
∴PQ=﹣n2+2n﹣(﹣n)=﹣n2+3n,
∴S△OPB=![]() (﹣n2+3n)=﹣
(﹣n2+3n)=﹣![]() (n﹣
(n﹣![]() )+
)+![]() ,
,
当n=![]() 时,S△OPB的最大值为
时,S△OPB的最大值为![]() .
.
此时y=﹣n2+2n=![]() ,
,
∴P(![]() ,
,![]() );
);
(3)∵直线OA的解析式为y=x,
∴可设新的抛物线解析式为y=﹣(x﹣a)2+a,
联立![]() ,
,
∴﹣(x﹣a)2+a=x,
∴x1=a,x2=a﹣1,
即C、D两点间的横坐标的差为1,
∴CD=![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目