Question

已知：如图，在△ABC中，∠C=90°，∠B=30°，AC=6，点D在边BC上，AD平分∠CAB，E为AC上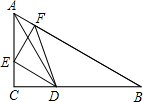的一个动点（不与A、C重合），EF⊥AB，垂足为F．
（1）求证：AD=DB；
（2）设CE=x，BF=y，求y关于x的函数解析式；
（3）当∠DEF=90°时，求BF的长？

Answer 1

（1）证明：在△ABC中，∵∠C=90°，∠B=30°，
∴∠CAB=60°，
又∵AD平分∠CAB，
∴∠DAB=∠DAC=

1

2

∠CAB=30°，
∴∠DAB=∠B，
∴AD=DB．

（2）在△AEF中，∵∠AFE=90°，∠EAF=60°，
∴∠AEF=30°，
∴AE=AC-EC=6-x，AF=

1

2

AE=

1

2

(6-x)，
在Rt△ABC中，∵∠B=30°，AC=6，
∴AB=12，
∴BF=AB-AF=12-

1

2

(6-x)=9+

1

2

x，
∴y=9+

1

2

x，
答：y关于x的函数解析式是y=9+

1

2

x（0＜x＜6）．

（3）当∠DEF=90°时，∠CED=180°-∠AEF-∠FED=60°，
∴∠EDC=30°，ED=2x，
∵∠C=90°，∠DAC=30°，
∴∠ADC=60°，
∴∠EDA=60°-30°=30°=∠DAE，
∴ED=AE=6-x．
∴有2x=6-x，得x=2，
此时，y=9+

1

2

×2=10，
答：BF的长为10．