题目内容
如图,在等腰Rt△ABC中,∠BAC=90°,BC=2,点E为线段AB上任意一点(E不与B重合),以CE为斜边作等腰Rt△CDE,连接AD,下列结论:
①∠BCE=∠ACD;②∠BCE=∠AED;③BE=AD;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
.
其中正确的结论有( )个.
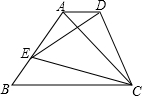
①∠BCE=∠ACD;②∠BCE=∠AED;③BE=AD;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为
| 3 |
| 2 |
其中正确的结论有( )个.
| A.1 | B.2 | C.3 | D.4 |

∵△ABC、△DCE都是等腰Rt△,
∴AB=AC=
BC=
,CD=DE=
CE;
∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB-∠ACE=∠DCE-∠ACE;
即∠ECB=∠DCA;故①正确;
②∵∠AED+∠DEC+∠BEC=180°,∠DEC=45°,
∴∠AED+∠BEC=135°,
又∵∠BCE+∠BEC=180°-∠B=180°-45°=135°,
∴∠AED=∠BCE,故此选项正确;
③∵
=
=
,
∴
=
;
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;
∴
=
,
∴BE≠AD,故此选项错误;
④∵△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,
即AD∥BC,故④正确;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;
△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC=
,AD=1;
故S梯形ABCD=
(1+2)×1=
,故⑤正确;
因此本题正确的结论是①②④⑤共4个,
故选:D.
∴AB=AC=
| ||
| 2 |
| 2 |
| ||
| 2 |
∠B=∠ACB=∠DEC=∠DCE=45°;
①∵∠ACB=∠DCE=45°,
∴∠ACB-∠ACE=∠DCE-∠ACE;
即∠ECB=∠DCA;故①正确;
②∵∠AED+∠DEC+∠BEC=180°,∠DEC=45°,
∴∠AED+∠BEC=135°,
又∵∠BCE+∠BEC=180°-∠B=180°-45°=135°,
∴∠AED=∠BCE,故此选项正确;
③∵
| CD |
| EC |
| AC |
| BC |
| ||
| 2 |
∴
| CD |
| AC |
| CE |
| BC |
由①知∠ECB=∠DCA,
∴△BEC∽△ADC;
∴
| AD |
| BE |
| ||
| 2 |
∴BE≠AD,故此选项错误;
④∵△BEC∽△ADC;
∴∠DAC=∠B=45°;
∴∠DAC=∠BCA=45°,
即AD∥BC,故④正确;
⑤△ABC的面积为定值,若梯形ABCD的面积最大,则△ACD的面积最大;
△ACD中,AD边上的高为定值(即为1),若△ACD的面积最大,则AD的长最大;
由④的△BEC∽△ADC知:当AD最长时,BE也最长;
故梯形ABCD面积最大时,E、A重合,此时EC=AC=
| 2 |
故S梯形ABCD=
| 1 |
| 2 |
| 3 |
| 2 |
因此本题正确的结论是①②④⑤共4个,
故选:D.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
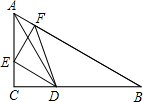 的一个动点(不与A、C重合),EF⊥AB,垂足为F.
的一个动点(不与A、C重合),EF⊥AB,垂足为F.