题目内容
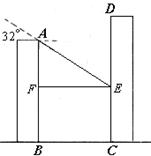
某住宅小区有一正南朝向的居民楼,如下图,该居民楼的一楼是高6m的小区超市,超市以上是居民住房.在该楼前方15m处准备盖一幢高20m的新楼.已知当地冬季正午的阳光与水平线夹角为32°.
(1)超市以上居民住房采光是否受到影响?为什么?
(2)若要使居民住房采光不受影响,两楼至少应相距多少米?
 (结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(1)超市以上居民住房采光是否受到影响?为什么?
(2)若要使居民住房采光不受影响,两楼至少应相距多少米?
 (结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)解:如图,设过A点的光线与CD交于点E,过点E作EF⊥AB于点F.则∠AEF=32o.
(1)设CE=x米,则AF=(20-x)米.…………………………2分
 在Rt△AEF中,tan∠AEF=,即tan32o=,
在Rt△AEF中,tan∠AEF=,即tan32o=,
∴20-x=15·tan32o
解得,x≈11………………………………4分
∵11>6,∴居民住房的采光有影响.…………5分
(2)若要使超市采光不受影响,则:
tan32o=,EF==14´="22.4" (m)……7分
∴两楼至少应相距23米,超市以上居民采光不受影响.………………8分
(1)设CE=x米,则AF=(20-x)米.…………………………2分
 在Rt△AEF中,tan∠AEF=,即tan32o=,
在Rt△AEF中,tan∠AEF=,即tan32o=,∴20-x=15·tan32o
解得,x≈11………………………………4分
∵11>6,∴居民住房的采光有影响.…………5分
(2)若要使超市采光不受影响,则:
tan32o=,EF==14´="22.4" (m)……7分
∴两楼至少应相距23米,超市以上居民采光不受影响.………………8分
略

练习册系列答案
相关题目
 ,
, ,从B点测得D点的仰角
,从B点测得D点的仰角 为60°,从A点测得D点
为60°,从A点测得D点 为30°,已知甲建筑物高AB=36米.
为30°,已知甲建筑物高AB=36米. )
)

 ,sinC=
,sinC= ,AC=5,则△ABC的面积是( )
,AC=5,则△ABC的面积是( )

 (2)
(2)
 tan30°-tan45°
tan30°-tan45°
 或
或

 的斜坡滑下,滑下距离S(米)与时间t(秒)之间的关系为S=
的斜坡滑下,滑下距离S(米)与时间t(秒)之间的关系为S= ,若滑动时间为4秒,则他下降的垂直高度为( )
,若滑动时间为4秒,则他下降的垂直高度为( ) 米 D
米 D 米
米