题目内容
.已知⊙O的半径为5,AB是弦,P是直线AB上的一点,PB=3, AB=8,则tan∠OPA的值为( )
| A.3 | B. | C. 或 或 | D.3或 |
D
析:点P是直线AB上的一点,则P可能在线段BE上,或BE的延长线上,因分两种情况进行讨论,过O作AB的垂线,根据三角函数的定义就可以求解即可求得答案.
解答: 解:作OE⊥AB,则EB=8×
解:作OE⊥AB,则EB=8× =4.
=4.
∵PB=3,∴EP=4-3=1.
又⊙O的半径为5,∴OE= =3.
=3.
当P在线段BE上时:tan∠OPA= =3;
=3;
当P在线段EB的延长线上时:设P是P1,则tan∠OP1A=3÷(1+3+3)= .
.
故答案为:D
解答:
 解:作OE⊥AB,则EB=8×
解:作OE⊥AB,则EB=8× =4.
=4.∵PB=3,∴EP=4-3=1.
又⊙O的半径为5,∴OE=
 =3.
=3.当P在线段BE上时:tan∠OPA=
 =3;
=3;当P在线段EB的延长线上时:设P是P1,则tan∠OP1A=3÷(1+3+3)=
 .
.故答案为:D

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目

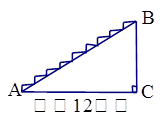
 (结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
(结果保留整数,参考数据:sin32o≈,cos32o≈,tan32o≈)
 , tan∠BCE=
, tan∠BCE= ,那么CE=
,那么CE= 
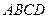 中,点
中,点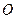 在对角线
在对角线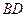 上,以
上,以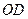 的长为半径的⊙
的长为半径的⊙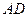 ,
,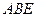 =∠
=∠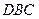 .
.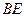 与⊙
与⊙
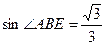 ,
,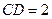 ,求⊙
,求⊙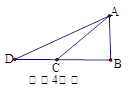
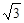 取1.732)
取1.732)