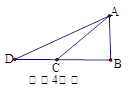
题目内容
平放在地面上的直角三角形铁板ABC的一部分被沙堆掩埋，其示意图如图所示．量
得角A为54°，斜边AB的长为2.1m，BC边上露出部分BD长为0.9m．求铁板BC边被掩
埋部分CD的长．（结果精确到0.1m）（参考数据：sin54°=0.81，cos54°=0.59，tan54°=1.38）
得角A为54°，斜边AB的长为2.1m，BC边上露出部分BD长为0.9m．求铁板BC边被掩
埋部分CD的长．（结果精确到0.1m）（参考数据：sin54°=0.81，cos54°=0.59，tan54°=1.38）
解：在△ABC中，∠C=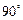
，
，
∵∠A=
，AB=2.1，
∴
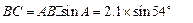
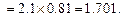（3分）
∵BD=0.9，
∴CD= BC－BD=1.701－0.9=0.801
0.8．
答：铁板BC边被掩埋部分CD的长约为0.8m． (5分)
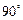，， ∵∠A=
，AB=2.1，∴
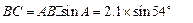
（3分）∵BD=0.9，
∴CD= BC－BD=1.701－0.9=0.801
0.8．答：铁板BC边被掩埋部分CD的长约为0.8m． (5分)
略
练习册系列答案
怎样学好牛津英语系列答案
相关题目
、
）
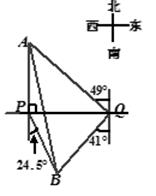
（结果保留整数，参考数据：sin32o≈，cos32o≈，tan32o≈）