题目内容
【题目】抛物线y＝x2+4x+3.
（1）求出该抛物线对称轴和顶点坐标．
（2）在所给的平面直角坐标系中用描点法画出这条抛物线．
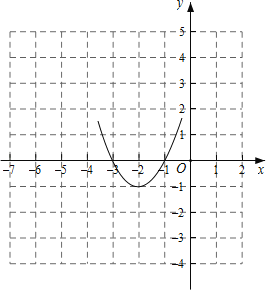
【答案】（1）对称轴为x＝﹣1，顶点坐标为（﹣2，﹣1）；（2）图象如图所示．见解析.
【解析】
(1)根据二次函数一般式，转化为二次函数顶点式，即可求出顶点坐标和对称轴.
(2)令y=0，计算出二次函数与x轴的交点坐标，在坐标系中标出，根据问题（1）确定顶点坐标的位置，然后从左至右依次连线即可解决.
（1）y＝x2+4x+3＝x2+4x+4﹣4+3＝（x+2）2﹣1，
顶点坐标为（﹣2，﹣1），
对称轴为x＝﹣1；
（2）当y＝0时，x2+4x+3＝0，
则（x+1）（x+3）＝0，
解得：x1＝﹣1，x2＝﹣3，
∴抛物线与x轴交于点（﹣1，0）（﹣3，0），
图象如图所示．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
