Question

【题目】如图1，在平面直角坐标系中，⊙O1与x轴相切于点A（﹣3，0），与y轴相交于B、C两点，且BC＝8，连接AB．

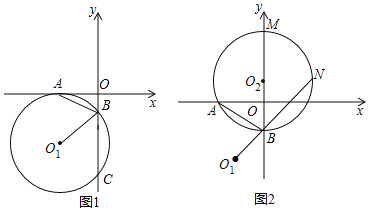
（1）求证：∠ABO1＝∠ABO；

（2）求AB的长；

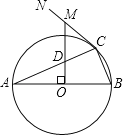
（3）如图2，⊙O2经过A、B两点，与y轴的正半轴交于点M，与O1B的延长线交于点N，求出BM﹣BN的值．

Answer 1

【答案】（1）见解析；（2）AB＝；（3）BM﹣BN的值为2．

【解析】

（1）连接AO1根据切线的性质，∠OAO1＝90°，因为∠AOB＝90°，根据平行线的判定方法，可以判定AO1∥OB，得到∠ABO＝∠O1AB，再根据O1A＝O1B，即可推导判断出∠ABO1＝∠ABO；

（2）过点O1作O1H⊥BC于H，判断出四边形AO1HO是矩形，根据勾股定理求出O1B与AB即可.

（3）作点B关于x轴的对称点B',根据对称性可知OB'＝OB＝1，AB＝AB'，根据等角的补角相等得出∠ABN＝∠AB'M，根据圆周角定理判断出∠AMB'＝∠N，最后判断△AMB'≌△ANB，得出结论MB'＝NB，最后计算求解即可.

（1）证明：如图，连接AO1，

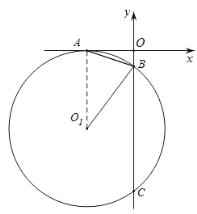
∵⊙O1与x轴相切于点A，

∴∠OAO1＝90°，

又∠AOB＝90°，

∴∠OAO1+∠AOB＝180°，

∴AO1∥OB，

∴∠ABO＝∠O1AB，

∵O1A＝O1B，

∴∠O1AB＝∠ABO1，

∴∠ABO1＝∠ABO；

（2）解：如图，过点O1作O1H⊥BC于H，

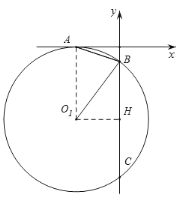
则CH＝BH＝BC＝4，

∴∠O1HO＝∠HOA＝∠OAO1＝90°，

∴四边形AO1HO是矩形，

∴AO1＝AO＝3，

∴在Rt△O1HB中，

，

∴HO＝O1A＝O1B＝5，

∴OB＝HO﹣BH＝1，

∴在Rt△AOB中，

；

（3）解：如图，作点B关于x轴的对称点B'，则点OB'＝OB＝1，AB＝AB'，

∴BB'＝2，∠AB'O＝∠ABO

∴由（1）知，∠ABO＝∠ABO1，

∴∠ABO1＝∠AB'O，

∴180°﹣∠ABO1＝180°﹣∠AB'O，

即∠ABN＝∠AB'M，

又∵,

∴∠AMB'＝∠N，

∴△AMB'≌△ANB（AAS），

∴MB'＝NB，

∴BM﹣BN＝BM﹣B'M＝BB'＝2，

∴BM﹣BN的值为2．