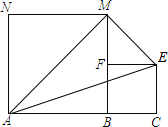题目内容
【题目】在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.
(1)求证:DM=DA;
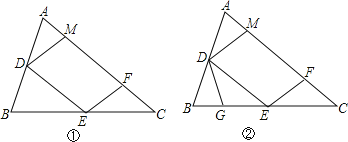
(2)点G在BE上,且∠BDG=∠C,如图②,求证:△DEG∽△ECF;
(3)在图②中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
【答案】(1)见解析(2)见解析(3)1
【解析】
试题分析:(1)证明∠A=∠DMA,用等角对等边即可证明结论;
(2)由D、E分别是AB、BC的中点,可知DE∥AC,于是∠BDE=∠A,∠DEG=∠C,又∠A=∠AFE,∠AFE=∠C+∠FEC,根据等式性质得∠FEC=∠GDE,根据有两对对应角相等的两三角形相似可证;
(3)通过证明△BDG∽△BED和△EFH∽△ECF,可得BGBE=EHEC,又BE=EC,所以EH=BG=1.
(1)证明:如图1所示,
∵DM∥EF,
∴∠AMD=∠AFE,
∵∠AFE=∠A,
∴∠AMD=∠A,
∴DM=DA;
(2)证明:如图2所示,
∵D、E分别是AB、BC的中点,
∴DE∥AC,
∴∠BDE=∠A,∠DEG=∠C,
∵∠AFE=∠A,
∴∠BDE=∠AFE,
∴∠BDG+∠GDE=∠C+∠FEC,
∵∠BDG=∠C,
∴∠GDE=∠FEC,
∴△DEG∽△ECF;
(3)解:如图3所示,
∵∠BDG=∠C=∠DEB,∠B=∠B,
∴△BDG∽△BED,
∴![]() ,
,
∴BD2=BGBE,
∵∠AFE=∠A,∠CFH=∠B,
∴∠C=180°﹣∠A﹣∠B=180°﹣∠AFE﹣∠CFH=∠EFH,
又∵∠FEH=∠CEF,
∴△EFH∽△ECF,
∴![]() ,
,
∴EF2=EHEC,
∵DE∥AC,DM∥EF,
∴四边形DEFM是平行四边形,
∴EF=DM=DA=BD,
∴BGBE=EHEC,
∵BE=EC,
∴EH=BG=1.




 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案【题目】实施素质教育以来,某中学立足于学生的终身发展,大力开发课程资源,在七年级设立六个课外学习小组,下面是七年级学生参加六个学习小组的统计表和扇形统计图,请你根据图表中提供的信息回答下列问题.
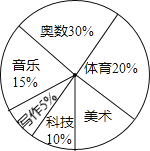
学习小组 | 体育 | 美术 | 科技 | 音乐 | 写作 | 奥数 |
人数 | 72 | 36 | 54 | 18 |
(1)七年级共有学生 人;
(2)在表格中的空格处填上相应的数字;
(3)表格中所提供的六个数据的中位数是 ;
(4)众数是 .