Question

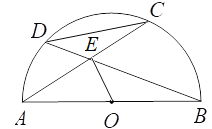
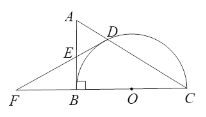
【题目】如图，在Rt△ABC中，∠ABC＝90o，以BC为直径的半圆⊙O交AC于点D，点E是AB的中点，连接DE并延长，交CB延长线于点F.

(1)判断直线DF与⊙O的位置关系，并说明理由；

(2)若CF＝8，DF＝4，求⊙O的半径和AC的长.

Answer 1

【答案】（1）相切，证明见解析；（2）.

【解析】

（1）连接OD，OE，证明△OBE≌△ODE，得到∠ODE＝∠OBE＝90°即OD⊥DE，从而得出结论；

（2）首先设⊙O半径为x，运用勾股定理得到方程，解方程可得圆的半径；证明△FBE∽△FDO，得出BE＝，由点E是AB中点，得出AB的长，再由勾股定理得出AC的长．

(1)相切

证明：连接OD，OE

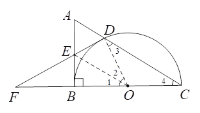
∵点E是AB中点，点O是BC中点

∴OE是△ABC的中位线，

∴OE∥AC

∴∠1＝∠4，∠2＝∠3

∵OC＝OD，

∴∠3＝∠4，

∴∠1＝∠2

∵OB＝OD，OE＝OE，

∴△OBE≌△ODE

∴∠ODE＝∠OBE＝90o

∴OD⊥DE，

∴直线DF与⊙O相切.

(2)设⊙O半径为x，则OD＝x，OF＝8－x

在Rt△FOD中，，

∴，

∴x＝3

∴⊙O半径为3

∵∠FBE＝∠FDO＝90°，∠F＝∠F，

∴△FBE∽△FDO，

∴，

∵BF＝FC－BC＝2，OD＝3，DF＝4，

∴BE＝，

∵点E是AB中点，

∴AB＝2BE＝3

在Rt△ABC中，AC＝＝