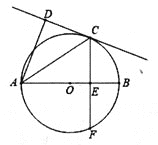
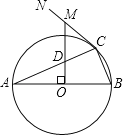
��Ŀ����
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��AC��y����3x+3![]() ��ֱ��AB��y��ax+b���ڵ�A����B����9��0����
��ֱ��AB��y��ax+b���ڵ�A����B����9��0����
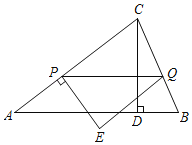
��1����F�ǵڶ�����λ��ֱ��AB�Ϸ���һ�㣬��F��FE��AB��E����F��FD��y�ύֱ��AB��D��DΪAB�е㣬���С�DFF���ܳ���12+4![]() ����MΪ�߶�AC��һ���㣬����EM����EM+
����MΪ�߶�AC��һ���㣬����EM����EM+![]() MC����Сֵ����ʱy������һ������G����|BG��MG|���ʱ����G�����ꣻ
MC����Сֵ����ʱy������һ������G����|BG��MG|���ʱ����G�����ꣻ
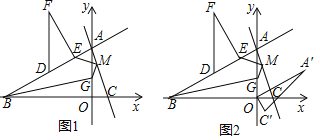
��2���ڣ�1��������£�����AOC��O��˳ʱ����ת60����õ���A��OC'����ͼ2�����߶�OA������x��ƽ�ƣ���ƽ�ƹ����е��߶�OA��ΪO��A������ƽ��ֱ������ϵ���Ƿ���ڵ�P��ʹ���Ե�O����A����E��PΪ������ı���Ϊ���Σ������ڣ��������P�����꣬�������ڣ���˵�����ɣ�
���𰸡���1��![]() -
-![]() ����0��
����0��![]() ������2�����ڣ���2
������2�����ڣ���2![]() ��2+3
��2+3![]() ����
����![]() ��9��2����6
��9��2����6![]() ��3����2��
��3����2��
��������
��1���� �����
����� ������C��x��Ĵ��ߡ�����M��y��Ĵ��ߣ������߽��ڵ�H��MH��MCcos����
������C��x��Ĵ��ߡ�����M��y��Ĵ��ߣ������߽��ڵ�H��MH��MCcos����![]() MC������E��M��H���㹲��ʱ��EM+MH��EM+
MC������E��M��H���㹲��ʱ��EM+MH��EM+![]() MC��С����
MC������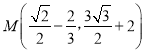 ��EM+
��EM+![]() MC��Сֵ��EH��xC��xE��
MC��Сֵ��EH��xC��xE��![]() ������M����y��ĶԳƵ�
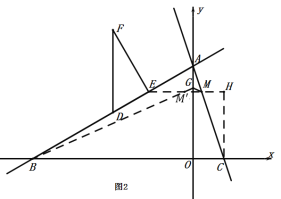
������M����y��ĶԳƵ�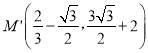 ������BM����y���ڵ�G�����ʱ|BG��MG|�������⣻
������BM����y���ڵ�G�����ʱ|BG��MG|�������⣻
��2�����߶�OA������x��ƽ����m����λ�����O����A��������ֱ�Ϊ��m��0����(![]() ��
��![]() )������
)������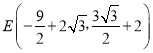 ��
��
�ٵ�O��A�������εı�ʱ����EP��P������O��A����OA��3![]() ��������⣻
��������⣻
�ڵ�O��A�������εĶԽ���ʱ�����P��a��b�������е㹫ʽ�ã�![]() ��
��![]() ����EO��EA������
����EO��EA������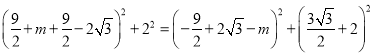 ��������⣮
��������⣮
��1����AC��![]() �ã���A��C������ֱ�Ϊ��
�ã���A��C������ֱ�Ϊ��![]() ��
��
��![]() ��
��![]()
��![]() ����
����![]()
��![]() ����A
����A![]() ������y��ax+b��
������y��ax+b��
�ã�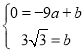 ����ã�
����ã�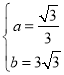
��ֱ��AB�ı���ʽΪ��![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
��FE��AB��FD��y�ᣬ���F����ABO��30����
�裺![]() ����
����![]() ��
��![]() ����DFF���ܳ���
����DFF���ܳ���![]() ��
��
��![]() ����ã�
����ã�![]() ��
��
DΪAB�е㣬���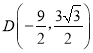 ��
��
s��ED��4����![]() ��
��
���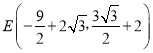 ��
��
����C��x��Ĵ��ߡ�����M��y��Ĵ��ߣ������߽��ڵ�H����ͼ1��
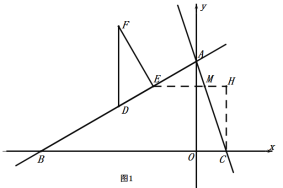
���HMC����ACO��������MH��MCcos����![]() MC��
MC��
����E��M��H���㹲��ʱ��EM+MH��EM+![]() MC��С��
MC����
��![]() ��
��
��M��ֱ��AC�ϣ����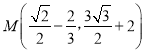 ��
��
����M����y��ĶԳƵ�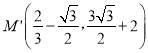 ������BM����y���ڵ�G����ͼ2��
������BM����y���ڵ�G����ͼ2��
���GΪ����ʱ|BG��MG|���
��![]() ��
��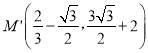 ���������һ�κ�������ʽ��y��kx+b��
���������һ�κ�������ʽ��y��kx+b��
��ã�![]()
�ʵ�G������Ϊ��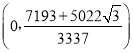 ��
��
���ϣ�EM+![]() MC��СֵΪ��
MC��СֵΪ��![]() ��
��![]() ��G����������0��
��G����������0��![]() ����
����
��2������AOC��O��˳ʱ����ת60����õ���A��OC'��
���OAA��Ϊ�߳�Ϊ4�ĵȱ������Σ����A����![]() ��
��![]() ����
����
���߶�OA������x��ƽ����m����λ��
���O����A��������ֱ�Ϊ��m��0������![]() ��
��![]() ��������
��������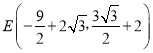 ��
��
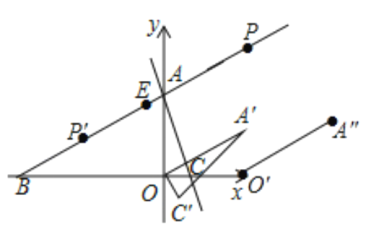
�ٵ�O��A�������εı�ʱ��
ֱ��OA����ֱ��AB����б�Ƕ���30������O��A����OA����AB��
��EP��P������O��A����OA��3![]() ��
��
��xP��xE��3![]() cos30����
cos30����![]() ��
��
�ʵ�P��2![]() ��2+3
��2+3![]() ����
����
ͬ����P����![]() ��2����
��2����
�ڵ�O��A�������εĶԽ���ʱ��
���P��a��b����
���е㹫ʽ�ã�![]() ��
��![]() ��
��
��EO��EA������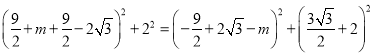 ��
��
��ã�![]() ��b����2��
��b����2��![]() ��6��
��6��
�ʣ�![]() 6
6![]() ��3��
��3��![]() ��
��
���P��6![]() ��3����2����
��3����2����
���ϣ���P����Ϊ����2![]() ��2+3
��2+3![]() ����
����![]() ��9��2����6
��9��2����6![]() ��3����2����
��3����2����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ����ѧ����ǰ��ij������ʦΪ���˽����ν̵ļס�������ѧ������������Ļ���֪ʶ������������������ѧ�����������Ļ���֪ʶ���м�⣬����100�֣��ִ�������ֱ������ȡ��20��ѧ���ļ��ɼ����������������ͷ������ɼ��÷���x��ʾ������Ϊ���飺
A.0��x��80��B.80��x��85��C.85��x��90��D.90��x��95��E.95��x��100������������˲�����Ϣ��
�װ�20��ѧ���ijɼ�Ϊ��
���� | 82 | 85 | 96 | 73 | 91 | 99 | 87 | 91 | 86 | 91 |
87 | 94 | 89 | 96 | 96 | 91 | 100 | 93 | 94 | 99 |
�Ұ�20��ѧ���ijɼ���D���е������ǣ�93��91��92��94��92��92��92
�ס��������ȡ��ѧ���ɼ�����ͳ�Ʊ�
�༶ | ���� | ���� |
ƽ���� | 91 | 92 |
��� | 91 | b |
���� | c | 92 |
���� | 41.2 | 27.3 |

����������Ϣ������������⣺
��1��ֱ��д������ͼ����a��b��c��ֵ��a���� ����b���� ����c���� ����
��2�������������ݣ�����Ϊ�ס������������ĸ����ѧ������֪ʶ��������Ϻã���˵�����ɣ�һ�����ɼ��ɣ���
��3�����ס�������������Ϊ125���Ҷ��μ��˴˴λ���֪ʶ��⣬���ƴ˴μ��ɼ����㣨x��95����ѧ�������Ƕ��٣�