Question

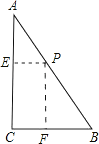
【题目】△ABC中，∠C＝90°，AB＝1，tanA＝，过AB边上一点P作PE⊥AC于E，PF⊥BC于F，E、F是垂足，则EF的最小值等于_____．

Answer 1

【答案】.

【解析】

根据已知∠A的正切值及勾股定理求出AC、BC长，可以利用勾股定理将EF2用PE长度表示，利用二次函数的最值问题求解，也可以利用矩形对角线相等转换成求CP最小值，利用垂线段最短和等面积法求解.

方法1：△ABC中，∠C＝90°，AB＝1，tanA＝，

∴AC＝，BC＝．

设PE＝x，则PF＝﹣x．

EF2＝PF2+PE2＝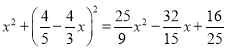

∴EF的最小值等于．

方法2：可知四边形CEPF是矩形，故EF＝CP

而只有当CP⊥AB时，CP才最小，

由AB＝1，tanA＝，

∴AC＝，BC＝．

由面积法可求出此时CP长

ACBC＝CPAB

即××＝CP×1

∴CP＝．

则EF的最小值等于．

故答案为：.