题目内容
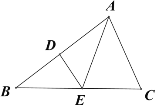
【题目】如图,△ABC内接于⊙O,直径BD交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.
(1)求证:OFDE=OE2OH;
(2)若⊙O的半径为12,且OE:OF:OD=2:3:6,求阴影部分的面积.(结果保留根号)

【答案】(1)证明:∵BD是直径,∴∠DAB=90°。
∵FG⊥AB,∴DA∥FO。∴△FOE∽△ADE。
∴![]() ,即OFDE=OEAD。
,即OFDE=OEAD。
∵O是BD的中点,DA∥OH,∴AD=2OH。∴OFDE=OE2OH。
(2)解:∵⊙O的半径为12,且OE:OF:OD=2:3:6,∴OE=4,ED=8,OF=6。
代入(1)中![]() ,得AD=12。∴OH=
,得AD=12。∴OH=![]() AD=6。
AD=6。
在Rt△ABC中,OB=2OH,∴∠OBH=30°,∴∠BOH=60°。
∴BH=BOsin60°=12×![]() 。
。
∴S阴影=S扇形GOB﹣S△OHB=![]() 。
。
【解析】(1)由BD是直径,根据圆周角定理,可得∠DAB=90°,又由FG⊥AB,可得FG∥AD,即可判定△FOE∽△ADE,根据相似三角形的对应边成比例,即可得![]() ,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OFDE=OE2OH。
,然后由O是BD的中点,DA∥OH,可得AD=2OH,则可证得OFDE=OE2OH。
(2)由⊙O的半径为12,且OE:OF:OD=2:3:6,即可求得OE,DE,OF的长,由![]() ,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB﹣S△OHB,即可求得答案。
,求得AD的长,又由在Rt△ABC中,OB=2OH,可求得∠BOH=60°,继而可求得BH的长,又由S阴影=S扇形GOB﹣S△OHB,即可求得答案。

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
【题目】甲乙两人在相同条件下完成了10次射击训练,两人的成绩如图所示。

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 方差/环 | |
甲 | ______ | 7 | 1.2 |
乙 | 7 | ______ | ______ |
(1)完成表格;
(2)根据训练成绩,你认为选派哪一名队员参赛更好?为什么?