题目内容
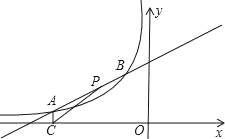
【题目】如图,已知A(﹣4,a),B(﹣1,2)是一次函数y1=kx+b与反比例函数y2=![]() (m<0)图象的两个交点,AC⊥x轴于C.
(m<0)图象的两个交点,AC⊥x轴于C.

(1)求出k,b及m的值.
(2)根据图象直接回答:在第二象限内,当y1>y2时,x的取值范围是 ________.
(3)若P是线段AB上的一点,连接PC,若△PCA的面积等于![]() ,求点P坐标.
,求点P坐标.
【答案】(1) k=![]() ,b=
,b=![]() ,m=﹣2;(2) ﹣4<x<﹣1;(3) 点P的坐标为(﹣2,
,m=﹣2;(2) ﹣4<x<﹣1;(3) 点P的坐标为(﹣2,![]() )
)
【解析】
(1)把点B的坐标代入y=![]() 即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
即可求出m的值,把点A的坐标代入反比例函数的解析式就可求出a,然后把A、B的坐标代入一次函数的解析式就可解决问题;
(2)运用数形结合的思想,结合图象即可解决问题;
(3)设点P的横坐标为xP,根据点A的坐标可得到AC的长,然后根据条件即可求出xP,然后将xP代入一次函数的解析式就可求出点P的坐标.
(1)把B(﹣1,2)代入y=![]() 得m=﹣1×2=﹣2,
得m=﹣1×2=﹣2,
把A(﹣4,a)代入y=﹣![]() 得a=﹣
得a=﹣![]() =
=![]() ,
,
把A(﹣4,![]() ),B(﹣1,2)代入y=kx+b,
),B(﹣1,2)代入y=kx+b,
得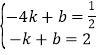 ,
,
解得:![]() ,
,
∴k=![]() ,b=
,b=![]() ,m=﹣2;
,m=﹣2;
(2)结合图象可得:在第二象限内,当y1>y2时,x的取值范围是﹣4<x<﹣1,
故答案为﹣4<x<﹣1;
(3)设点P的横坐标为xP,
∵AC⊥x轴,点A(﹣4,![]() ),
),
∴AC=![]() .
.
∵△PCA的面积等于![]() ,
,
∴![]() ×
×![]() ×[xP﹣(﹣4)]=
×[xP﹣(﹣4)]= ![]() ,
,
解得xP=﹣2,
∵P是线段AB上的一点,
∴yP=![]() ×(﹣2)+
×(﹣2)+![]() =
=![]() ,
,
∴点P的坐标为(﹣2,![]() ).
).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目