题目内容
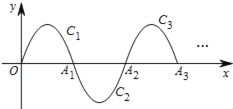
【题目】如图，我们把抛物线y=﹣x（x﹣3）（0≤x≤3）记为C1，它与x轴交于点O，A1将C1绕点A1旋转180°得C2，交x 轴于另一点A2；将C2绕点A2旋转180°得C3，交x 轴于另一点A3；…；如此进行下去，直至得C2016．①C1的对称轴方程是_____；②若点P（6047，m）在抛物线C2016上，则m=_____．
【答案】
，-2
【解析】
根据对称轴公式即可求得对称轴方程，观察图形可知第偶数号抛物线都在x轴下方，然后求出到抛物线C2016平移的距离，再根据向右平移横坐标加表示出抛物线C2016的解析式，然后把点P的坐标代入计算即可得解.
∵
，∴对称轴
，由图可知，抛物线C2016在x轴下方，相当于抛物线C1向右平移3×2015 ＝ 6045个单位得到，∴抛物线C13的解析式为
，∵点P（6047，m）在抛物线C2016上，∴
，故答案是①，②－2.
练习册系列答案
同步练习强化拓展系列答案
相关题目
【题目】一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：
售价x（元/千克） | … | 50 | 60 | 70 | 80 | … |
销售量y（千克） | … | 100 | 90 | 80 | 70 | … |
（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？
