题目内容
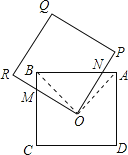
【题目】如图,两个边长都为2的正方形A BCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕D点旋转,那么它们重叠部分的面积为( )

A. 4 B. 2 C. 1 D. ![]()
【答案】C
【解析】
连OA,OB,设OR交BC于M,OP交AB于N,由四边形ABCD为正方形,得到OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,而四边形ORQP为正方形,得∠NOM=90°,所以∠MOB=∠NOA,则△OBM≌△OAN,即可得到S四边形MONB=S△AOB=![]() ×2×2=1.
×2×2=1.
连OA,OB,设OR交BC于M,OP交AB于N,如图,
∵四边形ABCD为正方形,
∴OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,
而四边形ORQP为正方形,
∴∠NOM=90°,
∴∠MOB=∠NOA,
∴△OBM≌△OAN,
∴S四边形MONB=S△AOB=![]() ×2×2=1,
×2×2=1,
即它们重叠部分的面积为1.
故选C.

练习册系列答案
相关题目
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分
组别 |
|
|
|
|
|
正确字数 |
|
|
|
|
|
人数 | 10 | 15 | 25 |
|
|

根据以上信息解决下列问题:
(1)在统计表中,![]() ,
,![]() ,并补全条形统计图.
,并补全条形统计图.
(2)扇形统计图中“![]() 组”所对应的圆心角的度数是 .
组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数