题目内容
【题目】如图,在△ABC中,A(1,-1)、B(l,-3)、C(4,-3).
(1)△![]()
![]()
![]() 是△ABC关于x轴的对称图形,则点A的对称点
是△ABC关于x轴的对称图形,则点A的对称点![]() 的坐标是_______;
的坐标是_______;
(2)将△ABC绕点(0,1)逆时针旋转90 °得到△A![]() B
B![]() C
C![]() ,则B点的对应点B
,则B点的对应点B![]() 的坐标是____;
的坐标是____;
(3)△![]()
![]()
![]() 与△A
与△A![]() B
B![]() C
C![]() 是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________
是否关于某条直线成轴对称?若成轴对称,则对称轴的解析式是_________________

【答案】(1) (-1,-1);(2) (4,2);(3) y=-x+1.
【解析】
(1)根据轴对称的性质及关于y轴对称的点的坐标特征解答即可.
(2)利用网格,将图形旋转90°,即可得到B2的坐标.
(3)连接△A1B1C1与△A2B2C2的对应点,对应点连线的垂直平分线即为所求直线.
(1)由图可知,A的对应点A1的坐标为(-1,-1).
故答案为:(-1,-1).
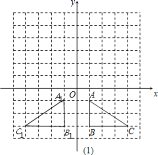
(2)由图可知,![]() 的坐标为(4,2);
的坐标为(4,2);
故答案为:(4,2).

(3)由图可见,直线过(0,1)和(1,0),
设函数解析式为y=kx+b,将(0,1)和(1,0)分别代入解析式得,
![]() ,
,
解得![]() ,
,
故的函数解析式为y=-x+1.
故答案为:y=-x+1.

练习册系列答案
相关题目