题目内容
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
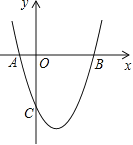
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
【答案】(1) y=x2-2x-3 ;(2) 对称轴是x=1,顶点坐标(1,-4) ;(3) (1+2![]() ,4)或(1-2
,4)或(1-2![]() ,4)或(1,-4)
,4)或(1,-4)
【解析】试题分析:(1)由于抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,那么可以得到方程x2+bx+c=0的两根为x=﹣1或x=3,然后利用根与系数即可确定b、c的值.
(2)根据S△PAB=8,求得P的纵坐标,把纵坐标代入抛物线的解析式即可求得P点的坐标.
试题解析:(1)∵抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,
∴方程x2+bx+c=0的两根为x=﹣1或x=3,
∴﹣1+3=﹣b,
﹣1×3=c,
∴b=﹣2,c=﹣3,
∴二次函数解析式是y=x2﹣2x﹣3.
(2)∵y=﹣x2﹣2x﹣3=(x﹣1)2﹣4,
∴抛物线的对称轴x=1,顶点坐标(1,﹣4).
(3)设P的纵坐标为|yP|,
∵S△PAB=8,
∴![]() AB|yP|=8,
AB|yP|=8,
∵AB=3+1=4,
∴|yP|=4,
∴yP=±4,
把yP=4代入解析式得,4=x2﹣2x﹣3,
解得,x=1±2![]() ,
,
把yP=﹣4代入解析式得,﹣4=x2﹣2x﹣3,
解得,x=1,
∴点P在该抛物线上滑动到(1+2![]() ,4)或(1﹣2
,4)或(1﹣2![]() ,4)或(1,﹣4)时,满足S△PAB=8.
,4)或(1,﹣4)时,满足S△PAB=8.

【题目】下表给出了代数式﹣x2+bx+c与x的一些对应值:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
﹣x2+bx+c | … | 5 | n | c | 2 | ﹣3 | ﹣10 | … |
(1)根据表格中的数据,确定b,c,n的值;
(2)设y=﹣x2+bx+c,直接写出0≤x≤2时y的最大值.
【题目】观察下面图形,解答下列问题:

(1)在上面第四个图中画出六边形的所有对角线;
(2)观察规律,把下表填写完整:
边数 | 三 | 四 | 五 | 六 | 七 | …… | n |
对角线 条数 | 0 | 2 | 5 | …… |
(3)若一个多边形的内角和为 1440°,求这个多边形的边数和对角线的条数.