Question

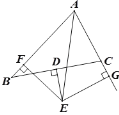
【题目】如图，在四边形ABCD中，AB⊥AD，CD⊥AD，将BC按逆时针方向绕点B旋转90°得到线段BE，连接AE．若AB=2，DC=4，则△ABE的面积为______．

Answer 1

【答案】2

【解析】

过点B作BF⊥DC与点F，过点E作EG⊥AB交AB的延长线于点G．求出四边形ABFD是矩形，根据矩形的对边相等可得AB=DF=2，然后求出CF=2，再求出∠CBF=∠EBG，然后利用“角角边”证明△BFC≌△BGE，根据全等三角形对应边相等可得EG=CF=2，再利用三角形的面积公式列式计算即可得解．

如图：过点B作BF⊥DC与点F，过点E作EG⊥AB交AB的延长线于点G．

∵AB⊥AD，CD⊥AD，BF⊥DC，∴∠D=∠BAD=∠BFD=90°，∴四边形ABFD是矩形，∴BF=AD，AB=DF=2，∠BFC=∠FBG=90°，

∵DC=4，DF=2，∴CF=DC﹣DF=4﹣2=2．

∵BC以点B为旋转中心，逆时针方向旋转90°至点E，∴∠CBE=90°，BC=BE，

∵∠EBC=∠FBG=90°，∴∠CBF=∠EBG=90°﹣∠CBG，

在△BFC和△BGE中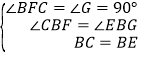，∵，∴△BFC≌△BGE（AAS），∴EG=CF=2，∴△ABE的面积=ABEG=×2×2=2．

故答案为：2．