题目内容
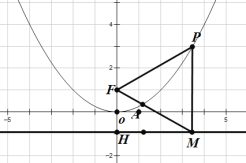
【题目】二次函数图象的顶点在原点O,经过点A(1,![]() );点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
);点F(0,1)在y轴上.直线y=﹣1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M.
求证:![]() PFM为等腰三角形;
PFM为等腰三角形;
(3)作PQ![]() FM于点Q,当点P从横坐标2013处运动到横坐标2017处时,请求出点Q运动的路径长.
FM于点Q,当点P从横坐标2013处运动到横坐标2017处时,请求出点Q运动的路径长.
【答案】(1)![]() ;(2)见解析;(3)2.
;(2)见解析;(3)2.
【解析】
(1)设抛物线的解析式为y=ax2,将点A的坐标代入求得a的值即可;
(2)由两点间的距离公式可求得PM和PF的长,从而得到PM=PF;
(3)由等腰三角形的性质可知点Q是FM的中点,从而得到OQ是△FHM的中位线,由三角形中位线的性质可求得当点P的横坐标为2013时,OQ=1006.5;当点P的横坐标为2017时,OQ=1008.5,故此可求得点Q运动的路径长.
(1)二次函数解析式为:y=ax2,
∵经过点A(1,![]() ),∴a=
),∴a=![]() ,∴二次函数的解析式y=
,∴二次函数的解析式y=![]() x2.
x2.
(2)∵点P是(1)中图象上的点,过点P作x轴的垂线与直线y=﹣1交于点M,
设P(x,![]() x2),则M(x,﹣1),∴PM=
x2),则M(x,﹣1),∴PM=![]() x2+1.
x2+1.
由两点间的距离公式可知:PF=![]() =
=![]() =
=![]() =
=![]() ,∴PF=PM ,即△PFM为等腰三角形.
,∴PF=PM ,即△PFM为等腰三角形.
(3)如图所示:过点P作PQ⊥FM,垂足为Q.
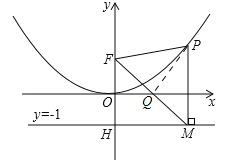
∵PF=PM,PQ⊥FM,∴FQ=QM.
∵OF=OH,FQ=QM,∴OQ∥HM,且OQ=![]() MH.
MH.
当点P的横坐标为2013时,![]()
当点P的横坐标为2017时,![]()
∴点Q运动的路径长:1008.5-1006.5=2.

练习册系列答案
相关题目