题目内容
如图,反比例函数y1的图象与一次函数y2的图象交于A,B两点,y2的图象与x轴交于点C,过A作AD⊥x轴于D,若OA=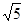 ,AD=
,AD=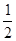 OD,点B的横坐标为
OD,点B的横坐标为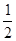 .
.
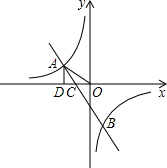
小题1:求一次函数的解析式及△AOB的面积
小题2:结合图象直接写出:当y1>y2时,x的取值范围
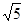 ,AD=
,AD=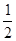 OD,点B的横坐标为
OD,点B的横坐标为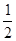 .
.
小题1:求一次函数的解析式及△AOB的面积
小题2:结合图象直接写出:当y1>y2时,x的取值范围
小题1:如图,连接OB,

在Rt△AOD中,OA=" 5" ,AD=
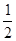 OD,且OD2+AD2=OA2,
OD,且OD2+AD2=OA2,代入解得AD=1,OD=2,故A(-2,1), 1分
设B点纵坐标为h,已知B点横坐标为
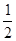 ,则(-2)×1=
,则(-2)×1=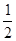 h,解得h=-4,
h,解得h=-4,故B(
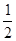 ,-4), 2分
,-4), 2分设直线AB解析式为y=kx+b,则 -2k+b="1" ,
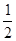 k+b=-4 ,得 k="-2" b=-3,
k+b=-4 ,得 k="-2" b=-3,直线AB解析式为y=-2x-3, 3分
由此可得C(-
 ,0),所以,S△AOB=S△AOC+S△BOC=
,0),所以,S△AOB=S△AOC+S△BOC= ; 5分
; 5分小题2:当y1>y2时,x的取值范围是:-2<x<0或x>
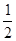 ; 7分
; 7分(1)AD=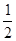 OD,根据此关系可在直角三角形中用勾股定理求得AD=1,OD=2,从而点A坐标可知;根据点B的横坐标求得B的纵坐标,待定系数法可求直线的解析式;△AOB的面积可以分割为两个三角形面积来求。
OD,根据此关系可在直角三角形中用勾股定理求得AD=1,OD=2,从而点A坐标可知;根据点B的横坐标求得B的纵坐标,待定系数法可求直线的解析式;△AOB的面积可以分割为两个三角形面积来求。
(2)观察图像。
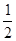 OD,根据此关系可在直角三角形中用勾股定理求得AD=1,OD=2,从而点A坐标可知;根据点B的横坐标求得B的纵坐标,待定系数法可求直线的解析式;△AOB的面积可以分割为两个三角形面积来求。
OD,根据此关系可在直角三角形中用勾股定理求得AD=1,OD=2,从而点A坐标可知;根据点B的横坐标求得B的纵坐标,待定系数法可求直线的解析式;△AOB的面积可以分割为两个三角形面积来求。(2)观察图像。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
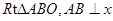 轴于点
轴于点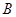 ,斜边
,斜边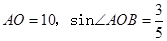 ,反比例函数
,反比例函数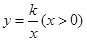 的图像经过
的图像经过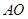 的中点
的中点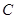 ,且与
,且与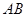 交于点
交于点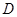 ,则点
,则点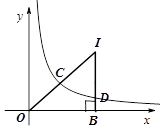
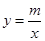 的图象和一次函数
的图象和一次函数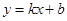 的图象的两个交点.
的图象的两个交点.
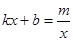 的解(请直接写出答案);
的解(请直接写出答案);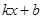 >
>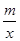 的解集(请直接写出答案).
的解集(请直接写出答案).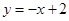 与
与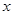 轴、
轴、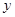 轴分别交于
轴分别交于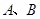 两点,过
两点,过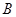 点作
点作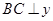 轴与双曲线
轴与双曲线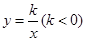 交于
交于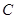 点,过
点,过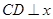 轴于
轴于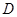 .若梯形
.若梯形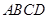 的面积为4,则
的面积为4,则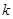 的值为_____.
的值为_____.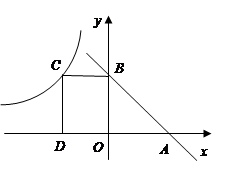
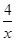 的图象上的是( )
的图象上的是( )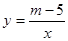 ,当
,当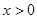 时,其图象位于第一象限,则m的取值范围是 ,此时
时,其图象位于第一象限,则m的取值范围是 ,此时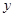 随
随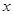 的增大而 。
的增大而 。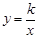 的图象过点(1,-2),则在图象的每一支上,y随x增大而 .(填‘增大’或‘减小’)
的图象过点(1,-2),则在图象的每一支上,y随x增大而 .(填‘增大’或‘减小’)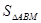 =2,则k的值是( )
=2,则k的值是( )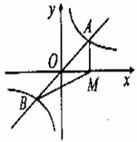
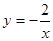 图象上有两点
图象上有两点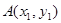 和
和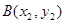 ,若
,若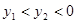 ,则
,则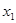 与
与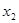 的关系是( )
的关系是( )


