题目内容
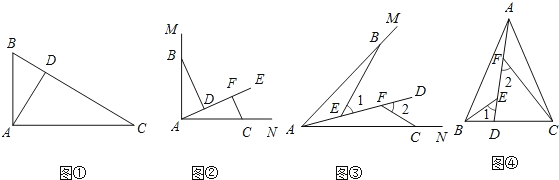
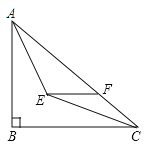
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的平分线相交于点E,过点E作
的平分线相交于点E,过点E作![]() 交AC于点F,则
交AC于点F,则![]() ;
;
【答案】![]()
【解析】
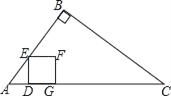
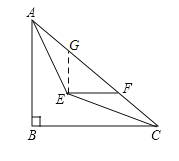
过E作EG∥AB,交AC于G,易得AG=EG,EF=CF,依据△ABC∽△GEF,即可得到EG:EF:GF=3:4:5,故设EG=3k=AG,则EF=4k=CF,FG=5k,根据AC=10,可得3k+5k+4k=10,即k=![]() ,进而得出EF=4k=
,进而得出EF=4k=![]() .
.
过E作EG∥AB,交AC于G,则∠BAE=∠AEG,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴∠CAE=∠AEG,
∴AG=EG,
同理可得,EF=CF,
∵AB∥GE,BC∥EF,
∴∠BAC=∠EGF,∠BCA=∠EFG,
∴△ABC∽△GEF,
∵∠ABC=90°,AB=6,BC=8,
∴AC=10,
∴EG:EF:GF=AB:BC:AC=3:4:5,
设EG=3k=AG,则EF=4k=CF,FG=5k,
∵AC=10,
∴3k+5k+4k=10,
∴k=![]() ,
,
∴EF=4k=![]() .
.
故答案是:![]() .
.

练习册系列答案
相关题目