题目内容
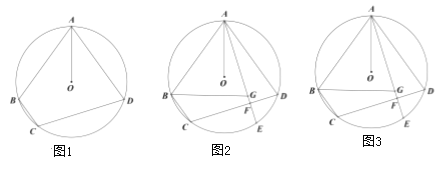
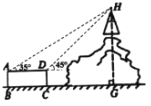
【题目】如图,AB为![]() 的直径,C、D为
的直径,C、D为![]() 上两点,且
上两点,且![]() ,垂足为F,直线CF交AB的延长线于点E,连接AC
,垂足为F,直线CF交AB的延长线于点E,连接AC
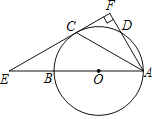
(1)判断EF与![]() 的位置关系,并说明理由:
的位置关系,并说明理由:
(2)若![]() ,
,![]() 的半径为4,求线段CF的长.
的半径为4,求线段CF的长.
【答案】(1)EF与⊙O相切,理由见解析;(2)CF=2![]()
【解析】
(1)连接OC,由题意可得∠OCA=∠FAC=∠OAC,可得OC∥AF,可得OC⊥EF,即EF是⊙O的切线;
(2)由直角三角形的性质可求AC=EC=4![]() ,即可求CF的长.
,即可求CF的长.
(1)EF与⊙O相切,理由如下:
如图,连接OC,
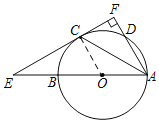
∵![]() ,
,
∴∠FAC=∠BAC,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OCA=∠FAC,
∴OC∥AF,
又∵EF⊥AF,
∴OC⊥EF
∴EF是⊙O的切线;
(2)∵∠FEA=30°,EF⊥AF,
∴∠FAE=60°,且∠FAC=∠BAC,
∴∠FAC=∠BAC=30°,
∴∠FEA=∠BAC=30°,
∴CE=AC,
∵OC⊥EF,∠FEA=30°,
∴CE=![]() OC=4
OC=4![]() ,
,
∴AC=4![]() ,
,
∵∠FAC=30°,EF⊥AF,
∴AC=2CF,
∴CF=2![]()

 阅读快车系列答案
阅读快车系列答案【题目】小明利用函数与不等式的关系,对形如![]() (
(![]() 为正整数)的不等式的解法进行了探究.
为正整数)的不等式的解法进行了探究.
(1)下面是小明的探究过程,请补充完整:
①对于不等式![]() ,观察函数
,观察函数![]() 的图象可以得到如下表格:
的图象可以得到如下表格:
|
|
|
|
|
|
由表格可知不等式![]() 的解集为
的解集为![]() .
.
②对于不等式![]() ,观察函数
,观察函数![]() 的图象可得到如下表格:
的图象可得到如下表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
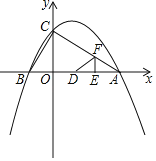
③对于不等式![]() ,请根据已描出的点画出函数
,请根据已描出的点画出函数![]() 的图象;
的图象;
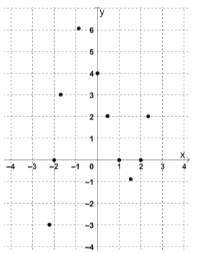
观察函数![]() 的图象,
的图象,
补全下面的表格:
|
|
|
|
|
|
|
|
由表格可知不等式![]() 的解集为 .
的解集为 .
小明将上述探究过程总结如下:对于解形如![]() (
(![]() 为正整数)的不等式,先将
为正整数)的不等式,先将![]() 按从大到小的顺序排列,再划分
按从大到小的顺序排列,再划分![]() 的范围,然后通过列表格的办法,可以发现表格中
的范围,然后通过列表格的办法,可以发现表格中![]() 的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
的符号呈现一定的规律,利用这个规律可以求这样的不等式的解集.
(2)请你参考小明的方法,解决下列问题:
①不等式![]() 的解集为 .
的解集为 .
②不等式![]() 的解集为 .
的解集为 .