ЬтФПФкШн
ЁОЬтФПЁПФГМвЕчЩњВњГЇМвШЅФъЯњЭљХЉДхЕФФГЦЗХЦЯДЭыЛњУПЬЈЕФЪлМл![]() ЃЈдЊЃЉгыдТЗн
ЃЈдЊЃЉгыдТЗн![]() жЎМфТњзуКЏЪ§ЙиЯЕ
жЎМфТњзуКЏЪ§ЙиЯЕ![]() ЃЌШЅФъЕФдТЯњЪлСПЛЇЃЈЭђЬЈЃЉгыдТЗн
ЃЌШЅФъЕФдТЯњЪлСПЛЇЃЈЭђЬЈЃЉгыдТЗн![]() жЎМфГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфжаСНИідТЕФЯњЪлЧщПіШчБэЃК
жЎМфГЩвЛДЮКЏЪ§ЙиЯЕЃЌЦфжаСНИідТЕФЯњЪлЧщПіШчБэЃК
дТЗнЃК | 1дТ | 5дТ |
ЯњЪлСПЃК | 3.9ЭђЬЈ | 4.3ЭђЬЈ |
ЃЈ1ЃЉЧѓИУЦЗХЦЯДЭыЛњдкШЅФъФФИідТЯњЭљХЉДхЕФЯњЪлН№ЖюзюДѓЃПзюДѓЪЧЖрЩйЃПЃЈЬсЪОЃКЯњЪлН№Жю=ЯњСПЁСЪлМлЃЉ
ЃЈ2ЃЉОЭГМЦКЭМЦЫу.ЕУЕНДЫЯДЭыЛњдкХЉДхЕиЧјЕФЯњЪлЪ§ОнЃЌШчБэЃК
ЯњЪлЪ§ОнаХЯЂБэ | ЪлМлЃЈдЊ/ЬЈЃЉ | ЯњСПЃЈЭђЬЈЃЉ | ВЙЬљН№ЖюЃЈЭђдЊЃЉ |
ШЅФъ12дТЗн | 2000 | 5 | / |
НёФъ2дТЗн |
|
| / |
НёФъ3дТЗн |
|
| 312 |
гЩгкЙњМвЪЕЪЉЁАМвЕчЯТЯчеўВпЁБЃЌЫљвдНёФъ3дТЗнЙњМвАДИУВњЦЗЪлМлЕФ13%ИјзгВЦеўВЙЬљЃЌЙВВЙЬљСЫ312ЭђдЊЃЌДгБэИёжаЃЌЮвУЧПЩвдПДГіЃКНёФъ3дТЗнгыНёФъ2дТЗнЯрБШНЯЃЌЪлМлБЃГжВЛБфЃЌЕЋЯњСПдіМгСЫ1.5ЭђЬЈ.НёФъ2дТЗнгыШЅФъ12дТЗнЯрБШНЯЃЌЪлМлЯТНЕСЫ![]() %ЃЌЯњСПЯТНЕСЫ1.5
%ЃЌЯњСПЯТНЕСЫ1.5![]() %ЃЛЧыгУ
%ЃЛЧыгУ![]() БэЪОБэИёжаЕФ
БэЪОБэИёжаЕФ![]() ЃЌ
ЃЌ![]() ЃЌВЂИљОнвбжЊЬѕМўЧѓГі
ЃЌВЂИљОнвбжЊЬѕМўЧѓГі![]() ЕФжЕ.
ЕФжЕ.
ЁОД№АИЁПЃЈ1ЃЉ7дТЃЌ10125ЭђдЊЃЛЃЈ2ЃЉ52.8.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЯШЧѓГівЛДЮКЏЪ§НтЮіЪНЃЌдйИљОнЯњЪлЮЪЬтЙЋЪНСаГіЖўДЮКЏЪ§НтЮіЪНМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнЬтвтСаГівЛдЊЖўДЮЗНГЬМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЩш![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЮЊ
ЕФКЏЪ§ЙиЯЕЪНЮЊ![]() ЃЈ
ЃЈ![]() ЃЉЃЌ
ЃЉЃЌ
ИљОнЬтвтЃЌЕУ![]()
НтЕУ![]() ЃЌЫљвдЃЌ
ЃЌЫљвдЃЌ![]() .
.
ЩшдТЯњЪлН№ЖюЮЊ![]() ЭђдЊЃЌ
ЭђдЊЃЌ
дђ![]()
![]()
![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЮЊ10125.
ШЁЕУзюДѓжЕЮЊ10125.
Д№ЃКИУЦЗХЦЯДЭыЛњдкШЅФъ7дТЯњЭљХЉДхЕФЯњЪлН№ЖюзюДѓЃЌзюДѓЪЧ10125ЭђдЊ.
ЃЈ2ЃЉИљОнБэИёЫљИјЪ§ОнЃЌЕУ
![]()
Сю![]() ЃЌдЗНГЬПЩЛЏЮЊ
ЃЌдЗНГЬПЩЛЏЮЊ![]()
НтЕУ![]()
Ыљвд![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉ
ЃЈЩсШЅЃЉ
Д№ЃК![]() ЕФжЕдМЮЊ52.8
ЕФжЕдМЮЊ52.8

ЁОЬтФПЁПаЁУїРћгУКЏЪ§гыВЛЕШЪНЕФЙиЯЕЃЌЖдаЮШч![]() (
(![]() ЮЊе§ећЪ§)ЕФВЛЕШЪНЕФНтЗЈНјааСЫЬНОП.
ЮЊе§ећЪ§)ЕФВЛЕШЪНЕФНтЗЈНјааСЫЬНОП.
(1)ЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећ:
ЂйЖдгкВЛЕШЪН![]() ЃЌЙлВьКЏЪ§
ЃЌЙлВьКЏЪ§![]() ЕФЭМЯѓПЩвдЕУЕНШчЯТБэИё:
ЕФЭМЯѓПЩвдЕУЕНШчЯТБэИё:
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ
ЕФНтМЏЮЊ![]() .
.
ЂкЖдгкВЛЕШЪН![]() ЃЌЙлВьКЏЪ§
ЃЌЙлВьКЏЪ§![]() ЕФЭМЯѓПЩЕУЕНШчЯТБэИё:
ЕФЭМЯѓПЩЕУЕНШчЯТБэИё:
|
|
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
ЂлЖдгкВЛЕШЪН![]() ,ЧыИљОнвбУшГіЕФЕуЛГіКЏЪ§
,ЧыИљОнвбУшГіЕФЕуЛГіКЏЪ§![]() ЕФЭМЯѓ;
ЕФЭМЯѓ;
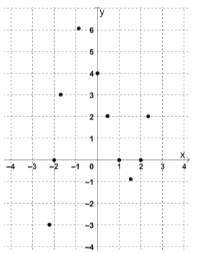
ЙлВьКЏЪ§![]() ЕФЭМЯѓ,
ЕФЭМЯѓ,
ВЙШЋЯТУцЕФБэИё:
|
|
|
|
|
|
|
|
гЩБэИёПЩжЊВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
аЁУїНЋЩЯЪіЬНОПЙ§ГЬзмНсШчЯТ:ЖдгкНтаЮШч![]() (
(![]() ЮЊе§ећЪ§)ЕФВЛЕШЪНЃЌЯШНЋ
ЮЊе§ећЪ§)ЕФВЛЕШЪНЃЌЯШНЋ![]() АДДгДѓЕНаЁЕФЫГађХХСаЃЌдйЛЎЗж
АДДгДѓЕНаЁЕФЫГађХХСаЃЌдйЛЎЗж![]() ЕФЗЖЮЇЃЌШЛКѓЭЈЙ§СаБэИёЕФАьЗЈЃЌПЩвдЗЂЯжБэИёжа
ЕФЗЖЮЇЃЌШЛКѓЭЈЙ§СаБэИёЕФАьЗЈЃЌПЩвдЗЂЯжБэИёжа![]() ЕФЗћКХГЪЯжвЛЖЈЕФЙцТЩЃЌРћгУетИіЙцТЩПЩвдЧѓетбљЕФВЛЕШЪНЕФНтМЏ.
ЕФЗћКХГЪЯжвЛЖЈЕФЙцТЩЃЌРћгУетИіЙцТЩПЩвдЧѓетбљЕФВЛЕШЪНЕФНтМЏ.
(2)ЧыФуВЮПМаЁУїЕФЗНЗЈЃЌНтОіЯТСаЮЪЬт:
ЂйВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .
ЂкВЛЕШЪН![]() ЕФНтМЏЮЊ .
ЕФНтМЏЮЊ .