Question

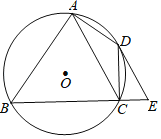
【题目】如图，M，N是以AB为直径的⊙O上的点，且弧AN＝弧BN，BM平分∠ABD，MC⊥BD于点C．

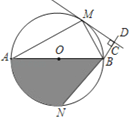
（1）求证：MC是⊙O的切线.

（2）若BC＝2，MC＝4，求⊙O的直径.

（3）在（2）的条件下，求阴影部分的周长．

Answer 1

【答案】（1）证明见解析；（2）⊙O的直径为10；（3）阴影部分的周长为10+5+．

【解析】

（1）连接OM，根据等腰三角形的性质可得∠OMB＝∠OBM，由BM平分∠ABD，可得∠OBM＝∠DBM，即可证明∠OMB＝∠DBM，可得OM∥BC，根据平行线的性质可得∠OMC＝90°，即可证明MC是⊙O的切线；（2）利用勾股定理可求出MB的长，由AB是直径可得∠AMB=90°，即可证明△ABM∽△MBC，根据相似三角形的性质即可求出AB的长；（3）根据圆周角定理可得AN=BN，由AB是直径可得∠ANB=90°，可得△ANB是等腰直角三角形，即可求出∠ABN＝45°，进而可得∠AON=90°，即可求出BN的长和的长，进而可得阴影部分周长.

（1）如图1，连接OM，

∵OM＝OB，

∴∠OMB＝∠OBM，

∵BM平分∠ABD，

∴∠OBM＝∠DBM，

∴∠OMB＝∠DBM，

∴OM∥BC，

∵MC⊥BD，

∴∠MCB＝90°，

∴∠OMC＝180°﹣∠MCB＝90°，

∴MC⊥OM，

∴MC是⊙O的切线.

（2）在Rt△MCB中，

MB＝＝＝2，

∵AB为⊙O的直径，

∴∠AMB＝90°＝∠MCB，

又∵∠ABM＝∠MBC，

∴△ABM∽△MBC，

∴，即，

∴AB＝10，

∴⊙O的直径为10.

（3）如图2，连接AN，ON，

∵，

∴AN＝BN，

又∵AB为⊙O的直径，

∴∠ANB＝90°，

∴△ANB是等腰直角三角形，

∴∠ABN＝45°，

∴∠AON＝90°，BN＝AB＝5，

∴＝，

∴AB+BN+＝10+5+，

∴阴影部分的周长为10+5+．