题目内容
【题目】关于二次函数![]() 的三个结论:①对任意实数m,都有
的三个结论:①对任意实数m,都有![]() 与
与![]() 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则
对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则![]() 或
或![]() ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则
;③若抛物线与x轴交于不同两点A,B,且AB≤6,则![]() 或
或![]() .其中正确的结论是( )
.其中正确的结论是( )
A.①②B.①③C.②③D.①②③
【答案】D
【解析】
由题意可求次函数y=ax2-4ax-5的对称轴为直线![]() ,由对称性可判断①;分a>0或a<0两种情况讨论,由题意列出不等式,可求解,可判断②;分a>0或a<0两种情况讨论,由题意列出不等式组,可求解,可判断③;即可求解.
,由对称性可判断①;分a>0或a<0两种情况讨论,由题意列出不等式,可求解,可判断②;分a>0或a<0两种情况讨论,由题意列出不等式组,可求解,可判断③;即可求解.
解:∵抛物线的对称轴为![]() ,
,
∴x1=2+m与x2=2-m关于直线x=2对称,
∴对任意实数m,都有x1=2+m与x2=2-m对应的函数值相等;
故①正确;
当x=3时,y=-3a-5,当x=4时,y=-5,
若a>0时,当3≤x≤4时,-3a-5<y≤-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴![]() ,
,
若a<0时,当3≤x≤4时,-5≤y<-3a-5,
∵当3≤x≤4时,对应的y的整数值有4个,
∴![]() ,
,
故②正确;
若a>0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≥0,
∴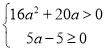 ,
,
∴![]() ;
;
若a<0,抛物线与x轴交于不同两点A,B,且AB≤6,
∴△>0,25a-20a-5≤0,
∴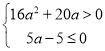
∴a<![]() ,
,
综上所述:当a<![]() 或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
或a≥1时,抛物线与x轴交于不同两点A,B,且AB≤6.
故③正确;
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目