题目内容
【题目】已知二次函数图象过点A(-2,0),B(4,0),C(0,4)
(1)求二次函数的解析式;
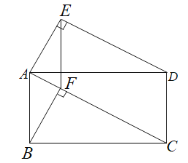
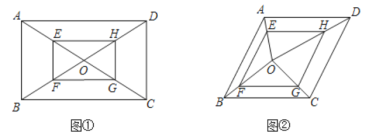
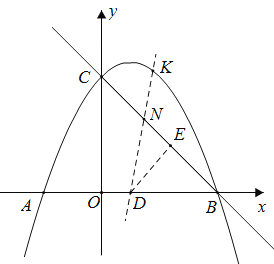
(2)如图,当点P为AC的中点时,在线段PB上是否存在点M,使得∠BMC=90°?若存在,求出点M的坐标,若不存在,请说明理由.
(3)点K在抛物线上,点D为AB的中点,直线KD与直线BC的夹角为锐角![]() ,且tan
,且tan![]() =
=![]() ,求点K的坐标.
,求点K的坐标.

【答案】(1)![]() ;(2)线段上存在
;(2)线段上存在![]() ,使得
,使得![]() ,理由详见解析;(3)抛物线上符合条件的点
,理由详见解析;(3)抛物线上符合条件的点![]() 坐标为:
坐标为: ![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)设二次函数的解析式为![]() ,将点C坐标代入可求解;
,将点C坐标代入可求解;
(2)利用中点坐标公式可求P(﹣1,2),点Q(2,2),由勾股定理可求BC的长,由待定系数法可求PB解析式,设点M![]() ,由两点距离公式可得
,由两点距离公式可得![]() ,可求
,可求![]() 或
或![]() ,即可求解;
,即可求解;
(3)过点D作DE⊥BC于点E,设直线DK与BC交于点N,先求出![]() ,
,![]() ,由锐角三角函数可求
,由锐角三角函数可求![]() ,分DK与射线EC交于点
,分DK与射线EC交于点![]() 和DK与射线EB交于
和DK与射线EB交于![]() 两种情况讨论,求出直线DK解析式,联立方程组可求点K坐标.
两种情况讨论,求出直线DK解析式,联立方程组可求点K坐标.
解:(1)二次函数的图象过点![]()
设二次函数解析式为![]()
又二次函数的图象过点![]() ,
,
∴![]() ,即
,即![]()
故二次函数解析式为![]()
(2)线段上存在![]() ,使得
,使得![]() ,理由如下:
,理由如下:
设![]() 中点为
中点为![]() ,由题意,易知
,由题意,易知![]() 的坐标为
的坐标为![]() ,
,![]()
若![]() ,则
,则![]()
∵![]() ,∴≈
,∴≈![]() 的中点
的中点![]() 为
为![]()
设![]() 所在的直线为
所在的直线为![]() ,则
,则![]() ,得
,得![]()
![]() 所在的直线为
所在的直线为![]()
![]() 在线段
在线段![]() 上,设
上,设![]() 的坐标为
的坐标为![]() ,其中
,其中![]()
如图1,分别过![]() ,
,![]() 作
作![]() 轴与
轴与![]() 轴的垂线
轴的垂线![]() ,
,![]() ,设
,设![]() ,
,![]() 相交于点
相交于点![]() ,
,
∴![]()
![]()
∵![]()
∴![]()
整理得![]() ,解得
,解得![]() 或
或![]()
当![]() 时,
时,![]() ,
,![]() 重合,不合题意(舍去)
重合,不合题意(舍去)
∴![]() ,则
,则![]() 的坐标为
的坐标为![]()
故线段![]() 上存在
上存在![]() ,使得
,使得![]()
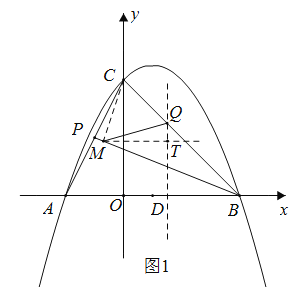
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,设直线
,设直线![]() 与
与![]() 交于点
交于点![]()
∵![]()
∴![]()
∵![]()
∴直线![]()
在![]() 中
中
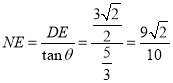
①若![]() 与射线
与射线![]() 交于点
交于点![]()
∴![]()
∴![]()
∴![]()
∴直线![]()
∴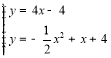
解得![]() 或
或![]()
②若![]() 与射线
与射线![]() 交于点
交于点![]()
∴![]()
∴![]()
∴![]()
∴直线![]()
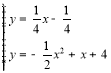 ,解得
,解得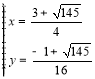 或
或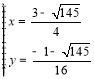
综上所述,抛物线上符合条件的点![]() 坐标为:
坐标为:
![]() 或
或![]() 或
或![]() 或
或![]() .
.

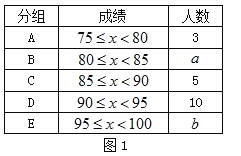
【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
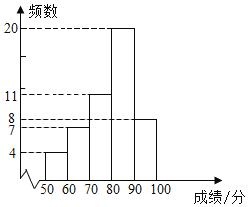
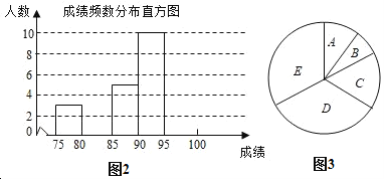
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.