题目内容
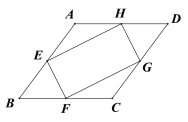
【题目】如图,在菱形ABCD中,点E、F、G、H分别是边AB、BC、CD和DA的中点,连接EF、FG、GH和HE.若EH=2EF,则下列结论正确的是
A. AB=![]() EF B. AB=2EF C. AB=
EF B. AB=2EF C. AB=![]() EF D. AB=
EF D. AB=![]() EF
EF
【答案】D
【解析】连接AC、BD交于点O,由菱形的性质可得OA=![]() AC,OB=
AC,OB=![]() BD,AC⊥BD,由中位线定理可得EH=
BD,AC⊥BD,由中位线定理可得EH=![]() BD,EF=
BD,EF=![]() AC,根据EH=2EF,可得OA=EF,OB=2EF,在Rt△AOB中,根据勾股定理即可求得AB=
AC,根据EH=2EF,可得OA=EF,OB=2EF,在Rt△AOB中,根据勾股定理即可求得AB=![]() EF,由此即可得到答案.
EF,由此即可得到答案.
连接AC、BD交于点O,
∵四边形ABCD是菱形,∴OA=![]() AC,OB=
AC,OB=![]() BD,AC⊥BD,
BD,AC⊥BD,
∵E、F、G、H分别是边AB、BC、CD和DA的中点,
∴EH=![]() BD,EF=
BD,EF=![]() AC,
AC,
∵EH=2EF,
∴OA=EF,OB=2OA=2EF,
在Rt△AOB中,AB=![]() =
=![]() EF,
EF,
故选D.

练习册系列答案
相关题目