题目内容
【题目】如图,已知抛物线![]() 经过
经过![]() ,
,![]() ,
,![]() 三点.
三点.
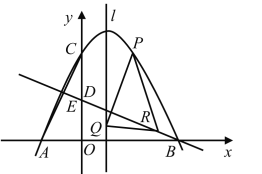
(1)求该抛物线的解析式;
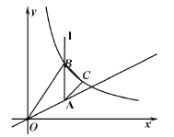
(2)经过点B的直线交y轴于点D,交线段![]() 于点E,若
于点E,若![]() .
.
①求直线![]() 的解析式;
的解析式;
②已知点Q在该抛物线的对称轴l上,且纵坐标为1,点P是该抛物线上位于第一象限的动点,且在l右侧.点R是直线![]() 上的动点,若
上的动点,若![]() 是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
是以点Q为直角顶点的等腰直角三角形,求点P的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②(2,4)或(
;②(2,4)或(![]() ,
,![]() )
)
【解析】
(1)根据待定系数法求解即可;
(2)①过点E作EG⊥x轴,垂足为G,设直线BD的表达式为:y=k(x-4),求出直线AC的表达式,和BD联立,求出点E坐标,证明△BDO∽△BEG,得到![]() ,根据比例关系求出k值即可;
,根据比例关系求出k值即可;
②根据题意分点R在y轴右侧时,点R在y轴左侧时两种情况,利用等腰直角三角形的性质求解即可.
解:(1)∵抛物线![]() 经过点
经过点![]() ,
,![]() ,
,![]() ,代入,
,代入,
∴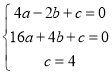 ,解得:
,解得: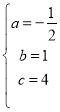 ,
,
∴抛物线表达式为:![]() ;
;
(2)①过点E作EG⊥x轴,垂足为G,
∵B(4,0),
设直线BD的表达式为:y=k(x-4),
设AC表达式为:y=mx+n,将A和C代入,
得:![]() ,解得:
,解得:![]() ,
,
∴直线AC的表达式为:y=2x+4,
联立: ,
,
解得: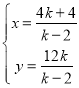 ,
,
∴E(![]() ,
,![]() ),
),
∴G(![]() ,0),
,0),
∴BG=![]() ,
,
∵EG⊥x轴,
∴△BDO∽△BEG,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴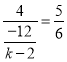 ,
,
解得:k=![]() ,
,
∴直线BD的表达式为:![]() ;
;
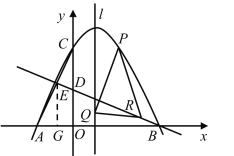
②由题意:设P(s,![]() ),1<s<4,
),1<s<4,
∵△PQR是以点Q为直角顶点的等腰直角三角形,
∴∠PQR=90°,PQ=RQ,
当点R在y轴右侧时,如图,
分别过点P,R作l的垂线,垂足为M和N,
∵∠PQR=90°,
∴∠PQM+∠RQN=90°,
∵∠MPQ+∠PQM=90°,
∴∠RQN=∠MPQ,又PQ=RQ,∠PMQ=∠RNQ=90°,
∴△PMQ≌△QNR,
∴MQ=NR,PM=QN,
∵Q在抛物线对称轴l上,纵坐标为1,
∴Q(1,1),
∴QN=PM=1,MQ=RN,
则点P的横坐标为2,代入抛物线得:y=4,
∴P(2,4);
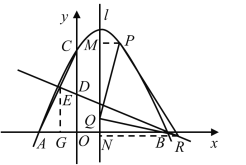
当点R在y轴左侧时,
如图,分别过点P,R作l的垂线,垂足为M和N,
同理:△PMQ≌△QNR,
∴NR=QM,NQ=PM,
设R(t,![]() ),
),
∴RN=![]() =QM,
=QM,
NQ=1-t=PM,
∴P(![]() ,2-t),代入抛物线,
,2-t),代入抛物线,
解得:t=![]() 或
或![]() (舍),
(舍),
∴点P的坐标为(![]() ,
,![]() ),
),
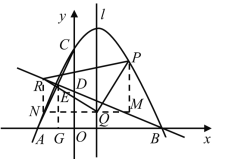
综上:点P的坐标为(2,4)或(![]() ,
,![]() ).
).

【题目】为了解某社区居民掌握民法知识的情况,对社区内的甲、乙两个小区各500名居民进行了测试,从中各随机抽取50名居民的成绩(百分制)进行整理、描述、分析,得到部分信息:
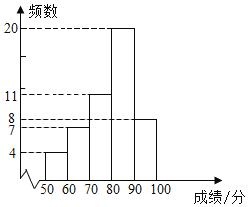
a.甲小区50名居民成绩的频数直方图如下(数据分成5组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100);
b.图中,70≤x<80组的前5名的成绩是:79 79 79 78 77
c.图中,80≤x<90组的成绩如下:
82 | 83 | 84 | 85 | 85 | 86 | 86 | 86 | 86 | 86 |
86 | 86 | 86 | 87 | 87 | 87 | 88 | 88 | 89 | 89 |
d.两组样本数据的平均数、中位数、众数、优秀率(85分及以上)、满分人数如下表所示:
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 满分人数 |
甲 | 78.58 | 84.5 | a | b | 1 |
乙 | 76.92 | 79.5 | 90 | 40% | 4 |
根据以上信息,回答下列问题:
(1)求表中a,b的值;
(2)请估计甲小区500名居民成绩能超过平均数的人数;
(3)请尽量从多个角度,分析甲、乙两个小区参加测试的居民掌握民法知识的情况.