Question

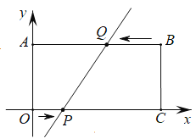
【题目】如图，一次函数y=kx+b的图象l与坐标轴分别交于点E，F，与双曲线y=﹣
（x＜0）交于点P（﹣1，n），且F是PE的中点．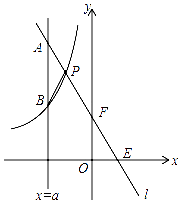

（1）求直线l的解析式；
（2）若直线x=a与l交于点A，与双曲线交于点B（不同于A），
①当a为何值时，△ABP是以点P为直角顶点的直角三角形？
②当a为何值时，PA=PB．

Answer 1

【答案】
（1）解：∵点P（﹣1，n）在反比例函数y=﹣ 图象上，

∴n=4，

∴P（﹣1，4），

∵F是PE的中点，

∴F（0，2），

∴ ，

∴ ，

∴y=﹣2x+2

（2）解：①∵△ABP是以点P为直角顶点的直角三角形，

∴∠APB=90°=∠EOF，

∵直线AB∥y轴，

∴∠BAP=∠OFE，

∴△APB∽△FOE，

∴ =

当x=a时，y=﹣2a+2，

∴A（a，﹣2a+2），

∵P（﹣1，4），

∴AP= = = |a+1|

当x=a时，y=﹣ ，

∴B（a，﹣ ），

∴AB=|﹣2a+2+ ，

∵直线EF的解析式为y=﹣2x+2，

∴E（1，0），F（0，2），

∴OF=2，EF= ，

∴ ，

∴a= （舍）或a=﹣1（舍）或a=﹣8，

即：a=﹣8时，△ABP是以点P为直角顶点的直角三角形；

②如图，

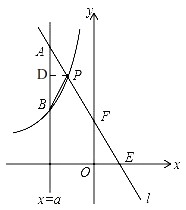
过P作PD⊥AB，垂足为点D，

∵P（﹣1，4），

∴D点的纵坐标为4，

∵PA=PB，

∴点D为AB的中点，

由题意知，A点的纵坐标为﹣2a+2，B点的纵坐标为 ，

∴ ，

解得a1=﹣2，a2=﹣1（舍去）．

∴当a=﹣2时，PA=PB

【解析】（1）将点P（﹣1，n）在代入反比例函数解析式可求得n的值，从而得到点P的坐标，然后再求得点F的坐标，接下来，利用待定系数法求解即可；
（2）①先判断出△APB∽△FOE，然后依据相似三角形对应边成比例的性质列方出求解即可；②利用线段的中点坐标建立方程求解即可.
【考点精析】掌握反比例函数的性质是解答本题的根本，需要知道性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大．