题目内容
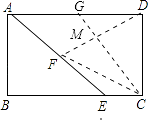
【题目】如图,在矩形ABCD中,AB=2 ![]() ,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为时,△CDF是等腰三角形.
,AD=4,点E是BC边上一个动点,连接AE,作DF⊥AE于点F,当BE的长为时,△CDF是等腰三角形. 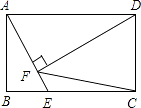
【答案】2或2 ![]() 或4﹣2
或4﹣2 ![]()
【解析】解:①CF=CD时,过点C作CM⊥DF,垂足为点M,
则CM∥AE,DM=MF,
延长CM交AD于点G,
∴AG=GD=2,
∴CE=2,
∴当BE=2时,△CDF是等腰三角形;②DF=DC时,则DF=DC=AB=2 ![]() ,
,
∵DF⊥AE,AD=2,
∴∠DAE=45°,
则BE=2 ![]() ,
,
∴当BE=2 ![]() 时,△CDF是等腰三角形;③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
时,△CDF是等腰三角形;③FD=FC时,则点F在CD的垂直平分线上,故F为AE中点.
∵AB=2 ![]() ,BE=x,
,BE=x,
∴AE= ![]() ,
,
AF= ![]() ,
,
∵△ADF∽△EAB,
∴ ![]() ,即
,即 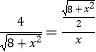 ,
,
解得:x=4﹣2 ![]() 或x=4+2
或x=4+2 ![]() (舍去);
(舍去);
∴当BE=4﹣2 ![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
综上,当BE=2或2 ![]() 或4﹣2
或4﹣2 ![]() 时,△CDF是等腰三角形.
时,△CDF是等腰三角形.
所以答案是:2或2 ![]() 或4﹣2
或4﹣2 ![]() .
.
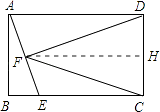
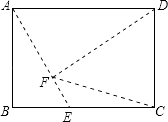
【考点精析】通过灵活运用等腰三角形的判定和矩形的性质,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;矩形的四个角都是直角,矩形的对角线相等即可以解答此题.

【题目】为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如下表.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | | |
处理污水量(吨/月) | 220 | 180 |
(1)求![]() 的值;
的值;
(2)由于受资金限制,运河综合治理指挥部决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有哪几种购买方案?每月最多能处理污水多少吨?