题目内容
【题目】已知点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
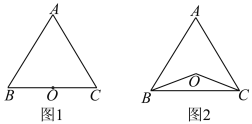
(1)如图1,若点O在边BC上,求证:∠ABC=∠ACB;
(2)如图2,若点O在△ABC的内部,则∠ABC=∠ACB成立吗?并说明理由;
(3)若点O在△ABC的外部,则∠ABC=∠ACB成立吗?请画图表示.
【答案】(1)见解析;(2)见解析;(3)见解析.
【解析】
(1)根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠ABC=∠ACB,即可得出答案;
(2)根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案;
(3)画出符合条件的两种情况:图③和图④,根据HL证Rt△OEB≌Rt△OFC,根据全等三角形的性质得出∠EBO=∠FCO,即可得出答案.
(1)证明:如图1,
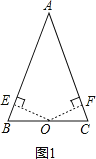
过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中,
![]() ,
,
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB;
(2)证明:如图2,过O作OE⊥AB于E,OF⊥AC于F,
则∠OEB=∠OFC=90°,
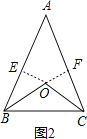
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABO=∠ACO,
∵∠OBC=∠OCB,
∴∠ABC=∠ACB;
(3)解:若O点在△ABC的外部,∠ABC=∠ACB不一定成立,
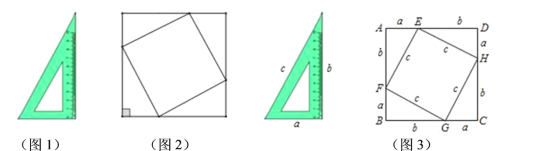
理由是:①当∠A的平分线和BC的垂直平分线重合时,如图3,
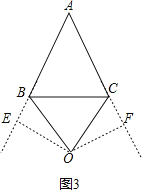
过O作OE⊥AB交AB的延长线于E,OF⊥AC交AC的延长线于F,
则∠OEB=∠OFC=90°,
∵点O到△ABC的两边AB、AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠EBO=∠FCO,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠ABC=180°-(∠OBC+∠EBO),∠ACB=180°-(∠OCB+∠FCO),
∴∠ABC=∠ACB;
②当∠A的平分线和BC的垂直平分线不重合时,如图④,

此时∠ABC和∠ACB不相等.

 阅读快车系列答案
阅读快车系列答案【题目】为了更好治理和净化运河,保护环境,运河综合治理指挥部决定购买10台污水处理设备.现有A、B两种型号的设备,其中每台的价格、月处理污水量如下表.经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格(万元/台) | | |
处理污水量(吨/月) | 220 | 180 |
(1)求![]() 的值;
的值;
(2)由于受资金限制,运河综合治理指挥部决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有哪几种购买方案?每月最多能处理污水多少吨?
【题目】某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
等级 | 分数 | 频数 | 频率 |
A | 90≤x≤100 | 6 | 0.15 |
B | 80≤x<90 | 20 | a |
C | 70≤x<80 | b | 0.2 |
D | 60≤x<70 | c | 0.15 |
合计 | 1 |
请你根据以上信息,解答下列问题: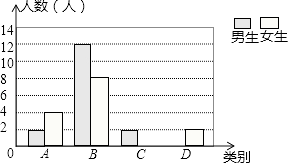
(1)a= , b= , c= , 并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.
【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .