Question

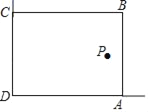
【题目】如图所示，在矩形ABCD中，点E在AD上，EC平分∠BED．

（1）试判断△BEC是否为等腰三角形，并说明理由．

（2）若AB=1，∠ABE=45°，求BC的长．

（3）在原图中画△FCE，使它与△BEC关于CE的中点O成中心对称，此时四边形BCFE是什么特殊平行四边形？请说明理由．

Answer 1

【答案】（1）是等腰三角形，理由见详解；（2）；（3）菱形，理由见详解.

【解析】

（1）易证∠BEC=∠BCE，从而判定△BCE是等腰三角形．

（2）由（1）知BC=BE，而BC是等腰直角△ABE的斜边，AB=BE，运用勾股定理可求．

（3）根据中心对称的性质，可知四边形BCFE是平行四边形，又BC=BE，得出BCFE是菱形．

解：（1）∵AD∥BC，

∴∠DEC=∠BCE，

∵∠DEC=∠BEC，

∴∠BEC=∠BCE，

∴△BCE是等腰三角形．

（2）∵在Rt△ABE中，∠ABE=45°，

∴∠AEB=∠ABE=45°，

∴AB=AE=1．

∴BE＝，

∴BC＝．

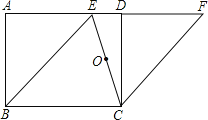
（3）如图，∵△FCE与△BEC关于CE的中点O成中心对称，

∴OB=OF，OE=OC，

∴四边形BCFE是平行四边形，

又∵BC=BE，

∴四边形BCFE是菱形．