题目内容
【题目】在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长为( )
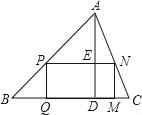
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
【答案】A
【解析】
由四边形PQMN是矩形,AD是BC边上的高,易证△BPQ∽△BAD,△APN∽ABC,可得出PQ:AD=BP:AB,PN:BC=AP:AB,BC=8,AD=6,据此可得出PQ,PN的值,故可得出矩形PQMN的周长.
∵四边形PQMN是矩形,AD是BC边上的高,
∴PQ⊥BC,AD⊥BC,PN∥BC
∴PQ∥AD,
∴△BPQ∽△BAD,△APN∽ABC,
∴PQ:AD=BP:AB,PN:BC=AP:AB
∴![]() ,
,
又∵PN=2PQ,BC=8cm,AD=6cm,
∴![]() ,
,
∴PQ=2.4
则PN=4.8,
∴矩形PQMN的周长=14.4cm.
故选A.

练习册系列答案
相关题目
【题目】某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
年度 | 2009 | 2010 | 2011 | 2012 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?