题目内容
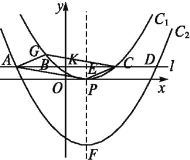
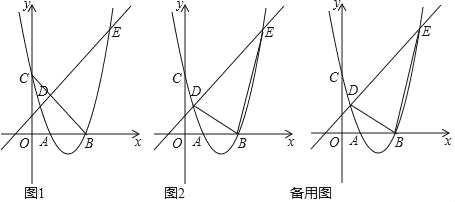
【题目】如图1,抛物线y=mx2﹣4mx+3m(m>0)与x轴交于A,B两点(点B在点A右侧).与y轴交点C,与直线l:y=x+1交于D、E两点,
(1)当m=1时,连接BC,求∠OBC的度数;
(2)在(1)的条件下,连接DB、EB,是否存在抛物线在第四象限上一点P,使得S△DBE=S△DPE?若存在,求出此时P点坐标及PB的长度;若不存在,请说明理由;
(3)若以DE为直径的圆恰好与x轴相切,求此时m的值.
【答案】(1)∠OBC=45°;(2)存在,P(2,﹣1),BP=![]() ;(3)m=
;(3)m=![]() 或﹣
或﹣![]() .
.
【解析】
(1)抛物线y=mx2-4mx+3m=m(x2-4x+3)=m(x-1)(x-3),把当m=1代入即可求解;
(2)S△DBE=S△DPE,∴点B、点P到直线DE的距离相等即可求解;
(3)求出DE的中点坐标为(![]() ,
,![]() ),即DE的长度,则圆的半径=
),即DE的长度,则圆的半径=![]() DE,利用
DE,利用![]() =
=![]() DE,即可求解.
DE,即可求解.
(1)∵抛物线y=mx2﹣4mx+3m=m(x2﹣4x+3)=m(x﹣1)(x﹣3),
∴A(1,0),B(3,0),
∴OB=3,
当m=1时,抛物线解析式为y=x2﹣4x+3,
∴C(0,3),∴OC=3,
∴OB=OC,在Rt△OBC中,∠BOC=90°,
∴∠OBC=45°;
(2)∵S△DBE=S△DPE,
∴点B、点P到直线DE的距离相等,即可求解,
∴BP∥DE,
由(1)知,B(3,0),
∵直线DE的解析式为y=x+1,
∴直线BP的解析式为y=x﹣3①,
∵抛物线解析式为y=x2﹣4x+3②,
联立①②解得,![]() 或
或![]() (点B的坐标,舍去),
(点B的坐标,舍去),
∴P(2,﹣1),
∵B(3,0),
∴BP=![]() =
=![]() ;
;
(3)∵点D,E在直线y=x+1上,
∴设D(x1,y1),E(x2,y2),
∵抛物线y=mx2﹣4mx+3m…③,
直线l:y=x+1…④,
联立③④得,mx2﹣4mx+3m=x+1,
∴mx2﹣(4m+1)x+(3m﹣1)=0,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴y1+y2=x1+x2+2=![]() ,
,
∴DE的中点坐标为(![]() ,
,![]() ),
),
DE=![]() =
=![]() =
=![]() =
=![]() ,
,
∵以DE为直径的圆恰好与x轴相切,
∴圆的半径=![]() DE,
DE,
则:![]() =
=![]()
![]() ,
,
整理得:28m2﹣12m﹣1=0,
解得:m=![]() 或﹣
或﹣![]() .
.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案