Question

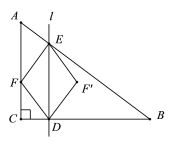
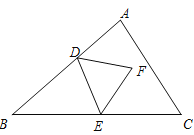
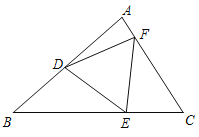
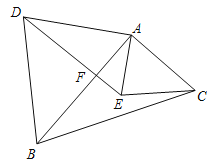
【题目】如图，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB与DE相交于点F，连接DB、CE．

（1）若，求∠AFD的度数；

（2）若∠ADE＝∠ABC，求证△ADB∽△AEC．

Answer 1

【答案】（1）90°；（2）证明见解析

【解析】

由，∠ADF＝∠EDA，证得 △ADF∽△EDA，从而得到 ∠AFD＝∠EDA=90°；

由∠ADE＝∠ABC，∠BAC＝∠DAE，证得 △ADE∽△ABC，从而得到，然后变形为 ，再求得∠DAB＝∠EAC，然后根据 ∠BAC＝∠DAE，即可证得.

（1）∵，∠ADF＝∠EDA，

∴△ADF∽△EDA．

∴∠AFD＝∠EDA．

∵∠DAE＝90°，∴∠AFD＝90°．

（2）∵∠ADE＝∠ABC，∠BAC＝∠DAE， ∴△ADE∽△ABC．

∴．

∴．

又∵∠BAC＝∠DAE，∴∠BAC－∠BAE＝∠DAE－∠BAE．

∴∠DAB＝∠EAC．

∴△ADB∽△AEC．