Question

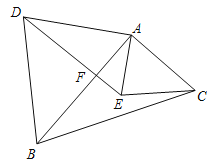
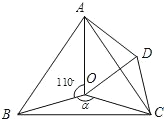
【题目】如图，点 O 是等边△ABC 内一点，∠AOB＝110°，∠BOC＝a．将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC，则△ADC≌△BOC，连接 OD．

（1）求证：△COD 是等边三角形；

（2）当α＝120°时，试判断 AD 与 OC 的位置关系，并说明理由；

（3）探究：当 a 为多少度时，△AOD 是等腰三角形？

Answer 1

【答案】（1）证明见解析；（2）证明见解析；（3）当 a 为 125°或 110°或 140°时，△AOD 是等腰三角形．

【解析】

（1）根据旋转得出CO=CD，∠DCO=60°，根据等边三角形的判定推出即可．
（2）求出∠ADO=∠COD=60°，根据平行线的判定推出即可．
（3）用∠α表示∠ADO、∠AOD、∠DAO，分为三种情况：①∠ADO=∠AOD，②∠ADO=∠OAD，③∠OAD=∠AOD，代入求出即可．

证明：（1）∵△ADC≌△BOC，

∴CO＝CD，

∵将△BOC 绕点 C 按顺时针方向旋转 60°得△ADC，

∴∠DCO＝60°，

∴△COD 是等边三角形．

（2）解：AD∥OC，

理由是：∵△DOC 是等边三角形，

∴∠CDO＝∠DOC＝60°，

∵∠α＝120°，△COB≌△CDA，

∴∠ADC＝∠COB＝120°，

∴∠ADO＝120°﹣60°＝60°，

∴∠ADO＝∠DOC＝60°，

∴AD∥OC．

（3）解：∠AOD＝360°﹣∠AOB﹣∠α﹣∠COD＝360°﹣110°﹣∠α﹣60°＝190°﹣∠α，∠ADO＝∠ADC﹣∠CDO＝∠α﹣60°，∠OAD＝180°﹣∠AOD﹣∠ADO＝180°﹣（∠α﹣60°）﹣（190°﹣∠α）＝50°， 若∠ADO＝∠AOD，即∠α﹣60°＝190°﹣∠α，

解得：∠α＝125°；

若∠ADO＝∠OAD，则∠α﹣60°＝50°， 解得：∠α＝110°；

若∠OAD＝∠AOD，即 50°＝190°﹣∠α， 解得：∠α＝140°；

即当 a 为 125°或 110°或 140°时，△AOD 是等腰三角形．