题目内容
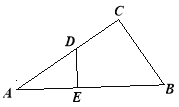
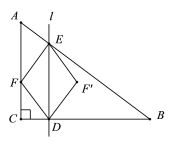
【题目】如图,在Rt△ABC中, ![]() ,
,![]() ,
,![]() ,直线l从与AC重合的位置开始以每秒
,直线l从与AC重合的位置开始以每秒![]() 个单位的速度沿CB方向平行移动,且分别与CB,AB边交于D,E两点,动点F从A开始沿折线AC
个单位的速度沿CB方向平行移动,且分别与CB,AB边交于D,E两点,动点F从A开始沿折线AC![]() CB
CB![]() BA运动,点F在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位,点F与直线l同时出发,设运动的时间为t秒,当点F第一次回到点A时,点F与直线 l同时停止运动.运动过程中,作点F关于直线DE的对称点,记为点
BA运动,点F在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位,点F与直线l同时出发,设运动的时间为t秒,当点F第一次回到点A时,点F与直线 l同时停止运动.运动过程中,作点F关于直线DE的对称点,记为点![]() ,若形成的四边形
,若形成的四边形![]() 为菱形,则所有满足条件的
为菱形,则所有满足条件的![]() 之和为_________.
之和为_________.
【答案】![]()
【解析】
首先结合题意画出图形,然后根据菱形的性质和相似三角形的性质分别从两种情况当P点在AC上时和当P在AB上时去分析求解,即可求得t的值.
如图1,当P点在AC上时,(0<t≤2)
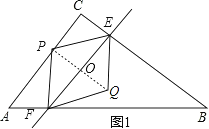
∴AP=3t,PC=6-3t,EC=![]() t,
t,
∴BE=8-![]() t,
t,
∵EF∥AC,
∴△FEB∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴EF=6-t.
∵四边形PEQF是菱形,
∴∠POE=90°,OE=![]() EF=3-
EF=3-![]() t,
t,
∵EF∥AC,∠C=90°,
∴∠OEC=90°,
∴四边形PCEO是矩形,
∴OE=PC.
∴3-![]() t=6-3t,
t=6-3t,
∴t=![]() ,
,
如图2,当P在AB上时(4<t<6),

∵四边形PFQE是菱形,
∴PE=PF,
∴∠PFE=∠PEF,
∵EF∥AC,∠C=90°,
∴∠FEB=∠FEP+∠PEB=90°,
∴∠B+∠EFB=90°,
∴∠B+∠FEP=90°,
∴∠PEB=∠B,
∴PE=PB.
∵PB=5(t-4),
∴BF=10(t-4),
∵sin∠B=![]() ,
,
∴![]() ,
,
∴EF=6t-24
∵CE=![]() t,
t,
∴BE=8-![]() t,
t,
∵△FEB∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴EF=6-t.
∴6-t=6t-24
解得t=![]() ;
;
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目