题目内容
【题目】如图,一段抛物线y=﹣x2+4(﹣2≤x≤2)为C1,与x轴交于A0,A1两点,顶点为D1;将C1绕点A1旋转180°得到C2,顶点为D2;C1与C2组成一个新的图象,垂直于y轴的直线l与新图象交于点P1(x1,y1),P2(x2,y2),与线段D1D2交于点P3(x3,y3),设x1,x2,x3均为正数,t=x1+x2+x3,则t的取值范围是( )

A. 6<t≤8 B. 6≤t≤8 C. 10<t≤12 D. 10≤t≤12
【答案】D
【解析】首先证明x1+x2=8,由2≤x3≤4,推出10≤x1+x2+x3≤12即可解决问题.
翻折后的抛物线的解析式为y=(x﹣4)2﹣4=x2﹣8x+12,
∵设x1,x2,x3均为正数,
∴点P1(x1,y1),P2(x2,y2)在第四象限,
根据对称性可知:x1+x2=8,
∵2≤x3≤4,
∴10≤x1+x2+x3≤12,
即10≤t≤12,
故选D.

【题目】今年5月13日是“母亲节”,某校开展“感恩母亲,做点家务”活动为了了解同学们在母亲节这一天做家务情况,学校随机抽查了部分同学,并用得到的数据制成如下不完整的统计表:
做家务时间(小时) | 人数 | 所占百分比 |
A组:0.5 | 15 | 30% |
B组:1 | 30 | 60% |
C组:1.5 | x | 4% |
D组:2 | 3 | 6% |
合计 | y | 100 |
(1)统计表中的x= ,y= ;
(2)小君计算被抽查同学做家务时间的平均数是这样的:
第一步:计算平均数的公式是![]() ,
,
第二步:该问题中n=4,x1=0.5,x2=1,x3=1.5,x4=2,
第三步:![]() =1.25(小时)
=1.25(小时)
小君计算的过程正确吗?如果不正确,请你计算出正确的做家务时间的平均数;
(3)现从C,D两组中任选2人,求这2人都在D组中的概率(用树形图法或列表法).
【题目】在春季运动会上,某学校教工组和学生组进行定点投篮比赛,每组均派五名选手参加,每名选手投篮十次,投中记1分,不中记零分,3分以上(含3分)视为合格,比赛成绩绘制成条形统计图如下:
投篮成绩条形统计图
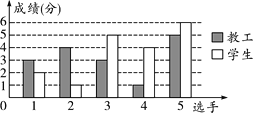
(1)请你根据条形统计图中的数据填写表格:
组别 | 平均数 | 中位数 | 方差 | 合格率 |
教工组 | ________ | 3 | ________ | 80% |
学生组 | 3.6 | ________ | 3.44 | 60% |
(2)如果小亮认为教工组的成绩优于学生组,你认为他的理由是什么?小明认为学生组成绩优于教工组,他的理由又是什么?
(3)若再让一名体育教师投篮后,六名教师成绩平均数大于学生组成绩的中位数,设这名体育教师命中m分,求m的值.