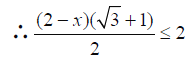Question

【题目】（数学概念）

若等边三角形的三个顶点D、E、F分别在△ABC的三条边上，我们称等边三角形DEF是△ABC的内接正三角形．

（概念辨析）

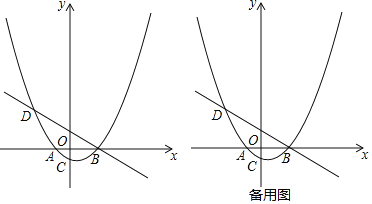
（1）下列图中△DEF均为等边三角形，则满足△DEF是△ABC的内接正三角形的是 ．

A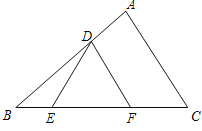．　　　　B．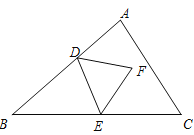

C．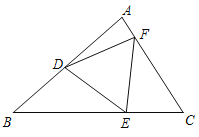

（操作验证）

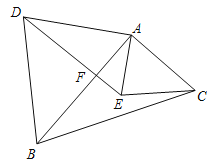
（2）如图①．在△ABC中，∠B＝60°，D为边AB上一定点（BC＞BD），DE＝DB，EM平分∠DEC，交边AC于点M，△DME的外接圆与边BC的另一个交点为N．

求证：△DMN是△ABC的内接正三角形．

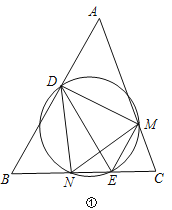
（知识应用）

（3）如图②．在△ABC中，∠B＝60°，∠A＝45°，BC＝2，D是边AB上的动点，若边BC上存在一点E，使得以DE为边的等边三角形DEF是△ABC的内接正三角形．设△DEF的外接圆⊙O与边BC的另一个交点为K，则DK的最大值为 ，最小值为 ．

Answer 1

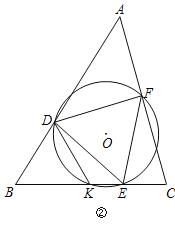
【答案】（1）C；（2）证明见解析；（3）2，．

【解析】

（1）由概念即可得；

（2）由等弧所对的圆周角相等和角平分线定理即可证得；

（3）

（1）由概念即可得答案为：C;

（2）∵DE=DB，∠B=60°

∴∠DEB=∠B=60°

∴∠DMN=∠DEB=60°

∴∠DEC=180°-∠DEB=120°

∵EM平分∠DEC

∴∠DEM= ∠DEC=60°

∴∠DNM=∠DEM==60°

∴∠NDM=180°-∠DMN-∠DNM=60°

∴∠NDM=∠DMN=∠DNM=60°

∴△DMN是正三角形

∵由概念得△DMN是△ABC的内接三角形

∴△DMN是△ABC的内接正三角形.

（3）2 ；

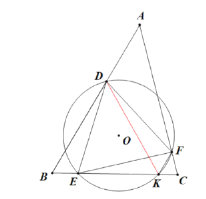
思路：①最大值

如图，当 K 与C 重合时， DK 最大，而△ BDK 是等边三角

形，所以 DK BK BC 2

②最小值

如右图，设 DK=BD=BK=x ，则CK=2- x .

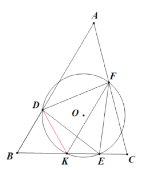
由手拉手模型：△ BDK 和△ DEF 都是等边三角形，且共点 D.易证△ BDE △ KDF .

∴ BE= KF

∵∠DKF=∠BDK= 60°，

∴ KF / / AB

∴

即

下面在图中求AB，

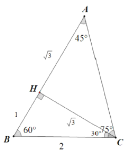
AB=,

∵BE≤BC=2，