题目内容
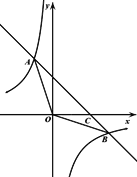
【题目】如图,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.
(1)求点B的坐标;
(2)求经过点A.O、B的抛物线的解析式;
(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,说明理由.


【答案】解:(1)如图,过B点作BC⊥x轴,垂足为C,则∠BCO=90°。
∵∠AOB=120°,∴∠BOC=60°。
又∵OA=OB=4,
∴OC=![]() OB=
OB=![]() ×4=2,BC=OBsin60°=
×4=2,BC=OBsin60°=![]() 。
。
∴点B的坐标为(﹣2,﹣![]() )。
)。
(2)∵抛物线过原点O和点A.B,
∴可设抛物线解析式为y=ax2+bx,将A(4,0),B(﹣2,﹣![]() )代入,
)代入,
得![]() ,解得
,解得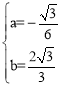 。
。
∴此抛物线的解析式为![]() 。
。
(3)存在。
如图,抛物线的对称轴是x=2,直线x=2与x轴的交点为D,
设点P的坐标为(2,y)。
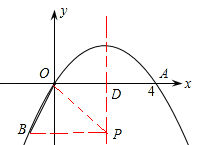
①若OB=OP,则22+|y|2=42,解得y=±![]() ,
,
当y=![]() 时,
时,
在Rt△POD中,∠PDO=90°,sin∠POD=![]() ,
,
∴∠POD=60°
∴∠POB=∠POD+∠AOB=60°+120°=180°,即P、O、B三点在同一直线上。
∴y=![]() 不符合题意,舍去。
不符合题意,舍去。
∴点P的坐标为(2,﹣![]() )。
)。
②若OB=PB,则42+|y+![]() |2=42,解得y=﹣
|2=42,解得y=﹣![]() 。
。
∴点P的坐标为(2,﹣![]() )。
)。
③若OP=BP,则22+|y|2=42+|y+![]() |2,解得y=﹣
|2,解得y=﹣![]() 。
。
∴点P的坐标为(2,﹣![]() )。
)。
综上所述,符合条件的点P只有一个,其坐标为(2,﹣![]() )。
)。
【解析】(1)首先根据OA的旋转条件确定B点位置,然后过B做x轴的垂线,通过构建直角三角形和OB的长(即OA长)确定B点的坐标。
(2)已知O、A、B三点坐标,利用待定系数法求出抛物线的解析式。
(3)根据(2)的抛物线解析式,可得到抛物线的对称轴,然后先设出P点的坐标,而O、B坐标已知,可先表示出△OPB三边的边长表达式,然后分①OP=OB、②OP=BP、③OB=BP三种情况分类讨论,然后分辨是否存在符合条件的P点。

 阅读快车系列答案
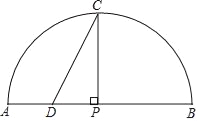
阅读快车系列答案【题目】24如图,P是弧AB所对弦AB上一动点,过点P作PC⊥AB交弧AB于点C,取AP中点D,连接CD.已知AB=6cm,设A,P两点间的距离为xcm,C.D两点间的距离为ycm.(当点P与点A重合时,y的值为0;当点P与点B重合时,y的值为3)
小凡根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小凡的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 0 | 2.2 |
| 3.2 | 3.4 | 3.3 | 3 |
(2)建立平面直角坐标系,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
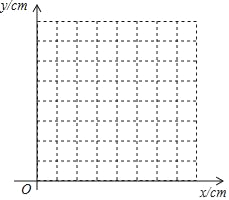
(3)结合所画出的函数图象,解决问题:当∠C=30°时,AP的长度约为 cm.