题目内容
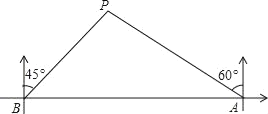
【题目】如图,在一笔直的海岸线上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿北偏西60°的方向行驶了30海里到达点P处,此时从B码头测得小船在北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
【答案】小船到B码头的距离是15![]() 海里,A、B两个码头间的距离是(15+15
海里,A、B两个码头间的距离是(15+15![]() )海里.
)海里.
【解析】
过P作PM⊥AB于M,求出∠PBM=45°,∠PAM=30°,求出PM,即可求出BM、BP.
如图,过P作PM⊥AB于M,则∠PMB=∠PMA=90°,
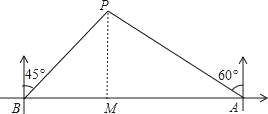
∵∠PBM=90°﹣45°=45°,∠PAM=90°﹣60°=30°,AP=30海里,
∴PM=![]() AP=15海里,AM=cos30°AP=15
AP=15海里,AM=cos30°AP=15![]() 海里,
海里,
∵∠BPM=∠PBM=45°,
∴BM=PM=15海里,
∴AB=AM+BM=(15+15![]() )海里,
)海里,
∴BP=![]() 海里,
海里,
即小船到B码头的距离是15![]() 海里,A、B两个码头间的距离是(15+15
海里,A、B两个码头间的距离是(15+15![]() )海里.
)海里.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目