题目内容
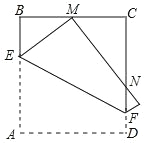
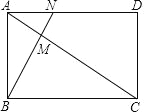
【题目】如图,已知矩形 ABCD 中,AB=1,BC=![]() ,点 M 在 AC 上,且 AM=
,点 M 在 AC 上,且 AM=![]() AC,连接并延长 BM 交 AD 于点 N.
AC,连接并延长 BM 交 AD 于点 N.
(1)求证:△ABC∽△AMB;
(2)求 MN 的长.
【答案】(1)见解析;(2)MN=![]() .
.
【解析】
(1)在Rt△ABC中利用勾股定理可求出AC的长度,进而可得出AM的长度,由AB、AM、AC的长度可得出![]() =
=![]() ,结合∠BAM=∠CAB即可证出△ABC∽△AMB;
,结合∠BAM=∠CAB即可证出△ABC∽△AMB;
(2)由△ABC∽△AMB可得出∠BMA=90°=∠BAN,利用勾股定理可求出BM的长度,结合∠ABM=∠NBA可证出△ABM∽△NBA,根据相似三角形的性质即可求出MN的长度.
(1)在 Rt△ABC 中,AB=1,BC=![]() ,
,
∴AC=2.
∵AM= ![]() AC,
AC,
∴AM= ![]() ,
,
∴![]() =
=![]() =
= ![]() .
.
又∵∠BAM=∠CAB,
∴△ABC∽△AMB.
(2)解:∵△ABC∽△AMB,
∴∠BMA=∠CBA=90°=∠BAN,
∴BM=![]() =
=![]() .
.
又∵∠ABM=∠NBA,
∴△ABM∽△NBA,
∴![]() =
=![]() ,即
,即 ![]() =
=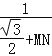 , 解得:MN=
, 解得:MN=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目