题目内容
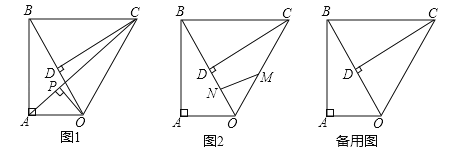
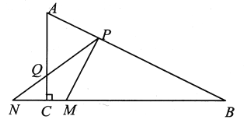
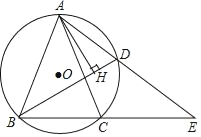
【题目】如图,△ABC内接于⊙O,BC=2,AB=AC,点D为![]() 上的动点,且cos∠ABC=
上的动点,且cos∠ABC=![]() .
.
(1)求AB的长度;
(2)在点D的运动过程中,弦AD的延长线交BC延长线于点E,问ADAE的值是否变化?若不变,请求出ADAE的值;若变化,请说明理由;
(3)在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
【答案】(1)![]() ;(2)不变,
;(2)不变,![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)作AM垂直于BC,由AB=AC,利用三线合一得到CM等于BC的一半,求出CM的长,再由cosB的值,利用锐角三角函数定义求出AB的长即可;
(2)连接DC,由等边对等角得到一对角相等,再由圆内接四边形的性质得到一对角相等,根据一对公共角,得到三角形EAC与三角形CAD相似,由相似得比例求出所求即可;
(3)在BD上取一点N,使得BN=CD,利用SAS得到三角形ACD与三角形ABN全等,由全等三角形对应边相等及等量代换即可得证.
解:(1)作AM⊥BC,
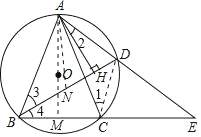
∵AB=AC,AM⊥BC,BC=2BM,
∴CM=![]() BC=1,
BC=1,
∵cosB=![]() ,
,
在Rt△AMB中,BM=1,
∴AB=![]() ;
;
(2)连接DC,
∵AB=AC,
∴∠ACB=∠ABC,
∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
∵∠ACE+∠ACB=180°,
∴∠ADC=∠ACE,
∵∠CAE公共角,
∴△EAC∽△CAD,
∴![]() ,
,
∴ADAE=AC2=10;
(3)在BD上取一点N,使得BN=CD,
在△ABN和△ACD中
 ,
,
∴△ABN≌△ACD(SAS),
∴AN=AD,
∵AN=AD,AH⊥BD,
∴NH=HD,
∵BN=CD,NH=HD,
∴BN+NH=CD+HD=BH.

【题目】春华中学为了解九年级学生的身高情况,随机抽测50名学生的身高后,所得部分资料如下(身高单位:![]() ,测量时精确到
,测量时精确到![]() ):
):
身高 | 148 | 151 | 154 | 155 | 157 | 158 | 160 | 161 | 162 | 164 |
人数 | 1 | 1 | 2 | 1 | 2 | 3 | 4 | 3 | 4 | 5 |
身高 | 165 | 166 | 167 | 168 | 170 | 171 | 173 | 175 | 177 | 179 |
人数 | 2 | 3 | 6 | 1 | 4 | 2 | 3 | 1 | 1 | 1 |
若将数据分成8组,取组距为![]() ,相应的频率分布表(部分)是:
,相应的频率分布表(部分)是:
分组 | 频数 | 频率 |
147.5~151.5 | 2 | 0.04 |
151.5~155.5 | 3 | 0.06 |
155.5~159.5 | 5 | 0.10 |
159.5~163.5 | 11 | 0.22 |
163.5~167.5 | ________ | ________ |
167.5~171.5 | 7 | 0.14 |
171.5~175.5 | 4 | 0.08 |
175.5~179.5 | 2 | 0.04 |
合计 | 50 | 1.00 |
请回答下列问题:
(1)样本数据中,学生身高的众数、中位数各是多少?
(2)填写频率分布表中未完成的部分;
(3)若该校九年级共有850名学生,请你估计该年级学生身高在![]() 及以上的人数.
及以上的人数.
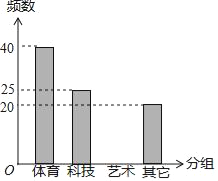
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?