��Ŀ����
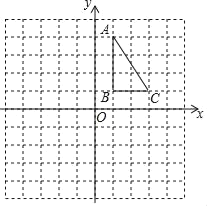
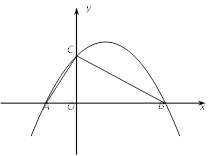
����Ŀ����ͼ����֪���κ���y��ax2��4ax��c��ͼ��x����A��B���㣨����A����B�����ࣩ����y���ڵ�C��0��3����
��1����tan��ACO��![]() ����������κ����ı���ʽ��
����������κ����ı���ʽ��
��2����OCΪOA��OB�ı������
����������κ����Ķ���ΪP������PBC�������
����MΪy����һ�㣬NΪƽ����һ�㣬�ʣ��Ƿ����������M��N��ʹ����M��N��B��CΪ������ı���Ϊ���Σ������ڣ���ֱ��д�����з��������ĵ�N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�(1) y����![]() x��x��3;(2)��
x��x��3;(2)��![]() ��;�ڼ�����.
��;�ڼ�����.
��������
��1������OC=3��tan��ACO=![]() ����֪OA�ij��ȣ������A��C��������κ����ı���ʽ��
����֪OA�ij��ȣ������A��C��������κ����ı���ʽ��
��2���ٸ���OCΪOA��OB�ı���������Ƴ���ACO�ס�BCO�����B��A�����꣬���κ����Ľ���ʽ����P�����������PBC����������ڷ�����������ۣ��ٸ�����������߶γ��ȣ�������ƽ�ƹ��ɵõ���N�����꣮
�⣺��1����Rt��AOC�У�C��0��3����tan��ACO=![]() ��
��
��A��-2��0����
����![]()
���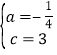
����κ����ı���ʽΪy=-![]() x2+x+3��
x2+x+3��
��2���١߶Գ���x=-![]() =2����ͼ1��ʾ��
=2����ͼ1��ʾ��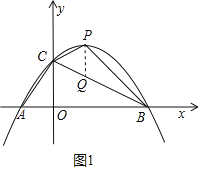
��OCΪOA��OB�ı�������ɵ���AOC�ס�COB��
���A��������m��0�������B��������4-m��0����
��OA=-m��OB=4-m��
��![]() ��
��
���m1=2+![]() ���ᣩ��m2=2-
���ᣩ��m2=2-![]() ��
��
��A��2-![]() ��0����B��
��0����B��![]() +2����
+2����
����![]() ��
��
���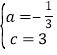
����κ����Ľ���ʽΪy=-![]() x2+
x2+![]() x+3��
x+3��
��P��2��![]() ����
����
��ֱ��BC�Ľ���ʽΪy=kx+b��
����![]() ��
��
���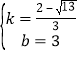 ��
��
��ֱ��BC�Ľ���ʽΪy=![]() ��
��
����P��y���ƽ���߽�BC�ڵ�Q��
��Q��2��![]() ����
����
��PQ=![]() ��
��
��S=![]() ��
��
�ڴ��ڣ������������
���һ����ͼ2��ʾ��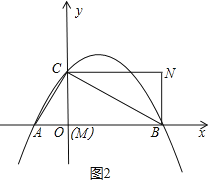
��ʱM��O�غϣ�
��N��![]() +2��3����
+2��3����
���������ͼ3��ʾ��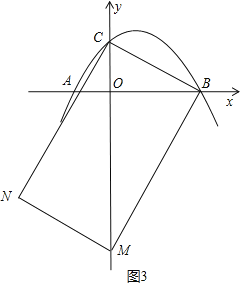
���ı���CBMNΪ���Σ����CBM=90����
���CBO=��OMB��
�ߡ�COB=��BOM��
���COB�ס�BOM��
��![]() ����
����![]()
���OM=![]() ��
��
��M��0��-![]() ����
����
�߶�NC���Դ�BMƽ�Ƶõ���
��B���CΪ��Ӧ�㣬��M���NΪ��Ӧ�㣬
��B�����ƶ���2+![]() ������λ�������ƶ�3����λ�õ���C��
������λ�������ƶ�3����λ�õ���C��
���M����NҲ��ͬ����ƽ�ƹ��ɣ�
��N��-2-![]() ��-
��-![]() -
-![]() ����
����
���ϣ���N������Ϊ��![]() +2��3����-
+2��3����-![]() -2��-
-2��-![]() -
-![]() ��
��

 ��У����ϵ�д�
��У����ϵ�д�