Question

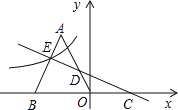
【题目】如图，抛物线交轴于、两点（点在点的左边），交轴于点，直线经过点与轴交于点，抛物线的顶点坐标为.

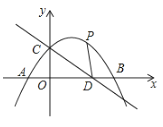
（1）请你求出的长及抛物线的函数关系式；

（2）求点到直线的距离；

（3）若点是抛物线位于第一象限部分上的一个动点，则当点运动至何处时，恰好使，请你直接写出此时的点坐标.

Answer 1

【答案】(1)5,或；(2)；（3）P.

【解析】

(1)求出点C，D的坐标，再用勾股定理求得CD的长；设抛物线为y=a(x-2)2+4，将点C坐标代入求得a，即可得出抛物线的函数表达式；
(2)过点B直线CD的垂线，垂足为H，在Rt△BDH中，利用锐角三角函数即可求得点B到直线CD的距离；
(3)构造等腰直角△EDC和K字型全等图形可得E点坐标，继而可求直线ED的解析式，而直线ED与抛物线的交点即为所求的点P．

解：(1)∵，

∴C(0，3)，D(4，0)，

∵∠COD＝90°，

∴CD＝=5．

设抛物线为y＝a(x﹣2)2+4，将点C(0，3)代入抛物线，

得3＝4a+4，

∴，

∴抛物线的函数关系式为或；

(2)解：过点B作BH⊥CD于H，

由，

可得x1＝﹣2，x2＝6，

∴点B的坐标为(6，0)，

∵OC＝3，OD＝4，CD＝5，

∴BD＝OB﹣OD＝6﹣4=2，

在Rt△DHB中，

∵BH＝BDsin∠BDH＝BDsin∠CDO＝2×=，

∴点B到直线CD的距离为．

(3作∠CDP＝45°交抛物线于点P,作EC⊥CD交射线DP于点E,作EF⊥y轴于F

∴∠CED＝∠CDP＝45°, ∴CE＝CD

∵∠ECF+∠OCD＝90°，∠ECF +∠FEC＝90°

∴∠OCD＝∠FEC

∵ ∠CFE＝∠DOC＝90°，

∴△≌△FEC(AAS)，

∴ CF＝OD＝4，EF＝OC＝3， OF=OC+CF=7

∴点E(3，7)，

由E(3，7)，D(4，0)，可得直线ED的解析式为：y＝﹣7x+28，

解方程组,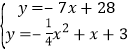

得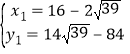 , 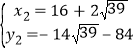(不合题意，舍去);

所以，此时P点坐标为(,)．