题目内容
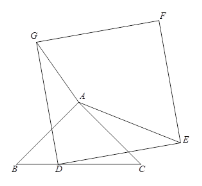
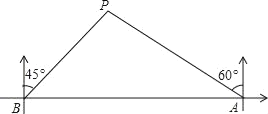
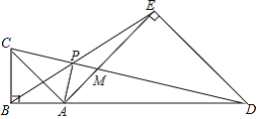
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧做等腰
的同侧做等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 分别交于点
分别交于点![]() .对于下列结论:①
.对于下列结论:①![]() ;②
;②![]() ;③2CB2=
;③2CB2=![]() .其中正确的是______.
.其中正确的是______.
【答案】①②③
【解析】
由等腰直角三角形的性质可得![]() ,
,![]() 即可得出
即可得出![]() ,即可证明
,即可证明![]() ,可得①正确;由①可得
,可得①正确;由①可得![]() ,根据
,根据![]() 可证明
可证明![]() ,根据相似三角形的性质即可证明②正确;由②可得
,根据相似三角形的性质即可证明②正确;由②可得![]() ,即可证明△MPA∽△MED,进而可得∠APM=∠AED=90°,根据平角的定义可求出∠CAE=90°,即可证明
,即可证明△MPA∽△MED,进而可得∠APM=∠AED=90°,根据平角的定义可求出∠CAE=90°,即可证明![]() ,根据相似三角形的性质和等腰直角三角形的性质即可得结论③正确.
,根据相似三角形的性质和等腰直角三角形的性质即可得结论③正确.
∵△ABC和△ADE是等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴∠BAC+∠CAE=∠EAD+∠CAE,
∴![]()
∴![]()
∴①正确
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]() ,
,
∴②正确
∵![]()
∴![]() ,即
,即![]() ,
,
又∵∠PMA=∠EMD,
∴△MPA∽△MED,
∴![]() ,
,
∵![]() ,∠ACM=∠ACM,
,∠ACM=∠ACM,
∴![]() ,
,
∴![]() ,
,
∴![]()
∵![]() ,AB=BC,
,AB=BC,
∴![]() .
.
所以③正确.
综上所述:正确的结论有①②③.
故答案为:①②③

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
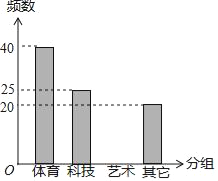
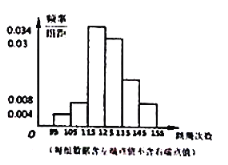
【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数 | 频率 | |
体育 | 40 | 0.4 |
科技 | 25 | a |
艺术 | b | 0.15 |
其它 | 20 | 0.2 |
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?