题目内容
【题目】如图,等腰△ABC中,AB=AC,BD,CE分别是边AC,AB上的中线,BD与CE相交于点O,点M,N分别为线段BO和CO的中点.求证:四边形EDNM是矩形.

【答案】见解析
【解析】试题分析:由题意得出ED是△ABC的中位线,得出ED∥BC,ED=![]() BC,由题意得出MN是△OBC的中位线,得出MN∥BC,MN=
BC,由题意得出MN是△OBC的中位线,得出MN∥BC,MN=![]() BC,因此ED∥MN,ED=MN,证明四边形EDNM是平行四边形,再由SAS证明△ABD≌△ACE,得出BD=CE,证出DM=EN,即可得出四边形EDNM是矩形.
BC,因此ED∥MN,ED=MN,证明四边形EDNM是平行四边形,再由SAS证明△ABD≌△ACE,得出BD=CE,证出DM=EN,即可得出四边形EDNM是矩形.
试题解析:证明:∵BD,CE分别是AC,AB边上的中线
∴AE=![]() AB,AD=
AB,AD=![]() AC,ED是△ABC的中位线
AC,ED是△ABC的中位线
∴ED∥BC,ED=![]() BC.
BC.
∵点M,N分别为线段BO和CO的中点
∴OM=BM,ON=CN,MN是△OBC的中位线
∴MN∥BC,MN=![]() BC
BC
∴ED∥MN,ED=MN
∴四边形EDNM是平行四边形
∴OE=ON,OD=OM.∵AB=AC
∴AE=AD.
在△ABD和△ACE中,
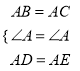
∴△ABD≌△ACE
∴BD=CE
∴EO+ON+CN=BM+OM+OD
∴3OE=3OM,
即OE=OM.
又∵DM=2OM,EN=2OE,
∴DM=EN
∴四边形EDNM是矩形

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目