题目内容
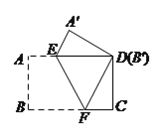
【题目】把一张长方形纸片按如图方式折叠,使顶点![]() 和点
和点![]() 重合,折痕为
重合,折痕为![]() .若
.若![]() ,
, ![]() .
.
求(![]() )
)![]() 的长.
的长.
(![]() )重叠部分
)重叠部分![]() 的面积.
的面积.
【答案】(1)3.4;(2)5.1
【解析】试题分析:(1)根据折叠的性质知:BF=DF,用DF表示出FC,在Rt△DCF中,利用勾股定理可求得DF的长;
(2)作FH⊥AD于点H,求得FH,由折叠的性质和平行线的性质证得∠EFD=∠DEF,得出DE=DF,进一步利用三角形的面积计算公式即可求解.
试题解析:
解:(1)设DF=x,
由折叠可知BF=DF=x,
∴FC=BC-BF=5-x,
∵四边形ABCD为长方形,
∴DC=AB=3,∠C=90°,AD∥BC,
在Rt△DCF中,∠C=90°,DF2=DC2+FC2
x2=32+(5-x)2
x=3.4,
∴DF=3.4cm;
(2)作FH⊥AD于点H,
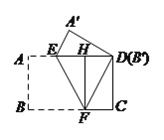
则FH=AB=3,
由折叠可知,
∠EFB=∠EFD,
∵AD∥BC,
∴∠DEF=∠EFB,
∴∠EFD=∠DEF,
∴ED=DF=3.4,
S△DEF=![]() ×DE×FH=
×DE×FH=![]() ×3.4×3=5.1.
×3.4×3=5.1.

练习册系列答案
相关题目
【题目】某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
种类 | 频数 | 频率 |
卡通画 | a |
|
时文杂志 | b | 0.16 |
武侠小说 | 50 | c |
文学名著 | d | e |
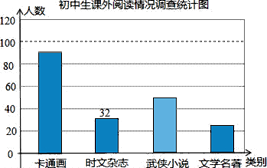
(1)这次随机调查了______名学生,统计表中a=______,d=______;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是______;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?